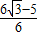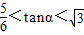题目内容
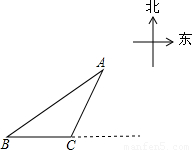
海中有一个小岛P,该岛四周12海里范围内(含12海里)是一个暗礁区.今有货轮由西向东航行,开始在A点观测P在北偏东60°.若行驶10海里后到达B点观测P在北偏东α(0<α<90°)处,若货船不改变航向,则当tanα为何值时,货轮会有触礁的危险,则根据以上数据可计算得tanα的值为( )
分析:货轮在A处时位于P岛的北偏东60°,在B处时位于北偏东α,根据题意,当∠PAB=30°时,可求出P到AB的最短距离,进而利用tan∠BPD=
=
,当α增大,则PD>12,即可得出答案.
| BD |
| PD |
6
| ||
| 6 |
解答: 解:过点P作PD⊥AB于点D,
解:过点P作PD⊥AB于点D,
∵货轮在A处时位于P岛的北偏东60°,在B处时位于北偏东α,
∴∠MAP=60°,∠NBP=∠BPD=α,
当PD=12,
∵∠PAB=30°,
∴AD=12
,
则tan∠BPD=
=
=
,
当α增大,则PD>12,
∴货轮会有触礁的危险时:0<tanα≤
故选:C.
 解:过点P作PD⊥AB于点D,
解:过点P作PD⊥AB于点D,∵货轮在A处时位于P岛的北偏东60°,在B处时位于北偏东α,
∴∠MAP=60°,∠NBP=∠BPD=α,
当PD=12,
∵∠PAB=30°,
∴AD=12
| 3 |
则tan∠BPD=
| BD |
| PD |
12
| ||
| 12 |
6
| ||
| 6 |
当α增大,则PD>12,
∴货轮会有触礁的危险时:0<tanα≤
6
| ||
| 6 |
故选:C.
点评:本题考查了解直角三角形的应用,解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线,求出tanα的最大值与最小值是解题关键.

练习册系列答案
相关题目
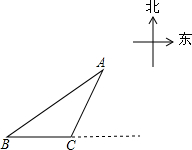 海中有一个小岛A,该岛四周10海里内有暗礁.今有货轮由西向东航行,开始在A岛南偏西60°的B处,往东行驶20海里后到达该岛的南偏西30°的C处.之后,货轮继续向东航行.你认为货轮继续向东航行图中会有触礁的危险吗?请说明你的理由.
海中有一个小岛A,该岛四周10海里内有暗礁.今有货轮由西向东航行,开始在A岛南偏西60°的B处,往东行驶20海里后到达该岛的南偏西30°的C处.之后,货轮继续向东航行.你认为货轮继续向东航行图中会有触礁的危险吗?请说明你的理由.