题目内容
（2001•荆州）在△ABC中，∠C=90°，BC=3，sinA=
，则AC的长是（ ）A．3
B．4
C．5
D．6
【答案】分析：根据三角函数的定义可求得AB的长，然后利用勾股定理直接解答．
解答：解：在Rt△ABC中，∠C=90°，
∴sin∠A=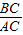
=
，
又BC=3，∴AC=5．
根据勾股定理知AC2=AB2-BC2=25-9=16，
∴AC=4．
故选B．
点评：本题主要考查了解直角三角形中三角函数和勾股定理的运用．
解答：解：在Rt△ABC中，∠C=90°，
∴sin∠A=
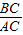=，又BC=3，∴AC=5．
根据勾股定理知AC2=AB2-BC2=25-9=16，
∴AC=4．
故选B．
点评：本题主要考查了解直角三角形中三角函数和勾股定理的运用．
练习册系列答案
名校课堂系列答案
相关题目
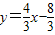与x轴交于点E，求四边形AECD的面积；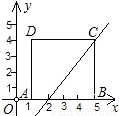
（2001•荆州）在双休日，某公司决定组织48名员工去附近的水上公园坐船游园，公司先派一个人去了解船只的租赁情况，这个人看到如下的租金价格表：
那么，怎样设计租船方案，才能使所付租金最少？（不得超载）
| 船型 | 每只限载人数 | 租金（元） |
| 大船 | 5 | 30 |
| 小船 | 3 | 20 |
（2001•荆州）在双休日，某公司决定组织48名员工去附近的水上公园坐船游园，公司先派一个人去了解船只的租赁情况，这个人看到如下的租金价格表：
那么，怎样设计租船方案，才能使所付租金最少？（不得超载）
| 船型 | 每只限载人数 | 租金（元） |
| 大船 | 5 | 30 |
| 小船 | 3 | 20 |
，则AC的长是（ ）