Question

（2011福建龙岩，24， 13分)如图，已知抛物线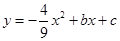与x轴相交于A、B两点，其对称轴为直线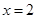，且与x轴交于点D，AO=1．

 

(1) 填空：b=_______。c=_______，

    点B的坐标为(_______，_______)：

(2) 若线段BC的垂直平分线EF交BC于点E，交x轴于点F．求FC的长；

(3) 探究：在抛物线的对称轴上是否存在点P，使⊙P与x轴、直线BC都相切？若存在，请求出点P的坐标；若不存在，请说明理由。

 

Answer 1

【答案】

24、（1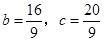），B(5，0)

（2）由（1）求得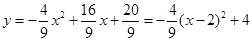

∴C（2，4）

∵E为BC的中点，由中点坐标公式求得E的坐标为（3.5，2）

易求直线BC的表达式为，整理得

设直线EF的表达式为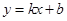

∵EF为BC的中垂线

∴EF⊥BC

∴

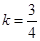
把E（3.5，2）代入求得

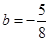
∴直线EF的表达式为，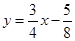

在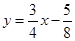中，令y=0，得

∴F(，0)

∴FC=FB=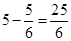

（3）存在，作∠OBC的平分线交DC于点P，则P满足条件。当然也可以作∠OBC的邻补角的平分线交DC于点P’，也满足条件，坐标求法一样。

设P（2，a），则P到x轴的距离等于P到直线BC的距离。（用到点到直线的距离公式）

∴

∴

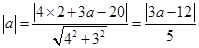
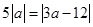
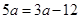∴或

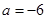解得或

∴P（2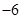，）或P（2，）。

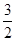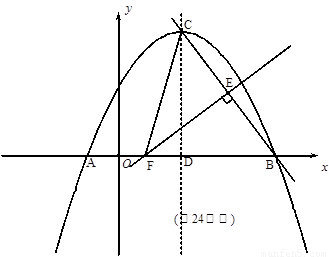
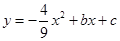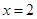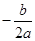【解析】（1）由抛物线，其对称轴为直线，即=2

得b值，且与x轴交于点D，AO=1得A、B坐标，代入一个即可求出c值。

（2）求出C的坐标，易求直线BC的表达式，

再由线段BC的垂直平分线EF交BC于点E，交x轴于点F，

得直线EF的表达式，令y=0，得，∴F(，0)

∴FC=FB=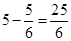

（3）作∠OBC的平分线交DC于点P，则P满足条件。当然也可以作∠OBC的邻补角的平分线交DC于点P，也满足条件，坐标求法一样。

 

【关键