题目内容
阅读下面的解题过程:
已知 ,求
,求 的值。
的值。
【解析】
由 知
知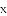

∴ ,故
,故 的值为
的值为
评注:该题的解法叫做“倒数法”,请你利用“倒数法”解下面的题目
已知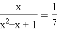 ,求
,求 的值。
的值。
练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
题目内容
阅读下面的解题过程:
已知 ,求
,求 的值。
的值。
【解析】
由 知
知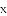

∴ ,故
,故 的值为
的值为
评注:该题的解法叫做“倒数法”,请你利用“倒数法”解下面的题目
已知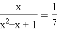 ,求
,求 的值。
的值。
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案