题目内容
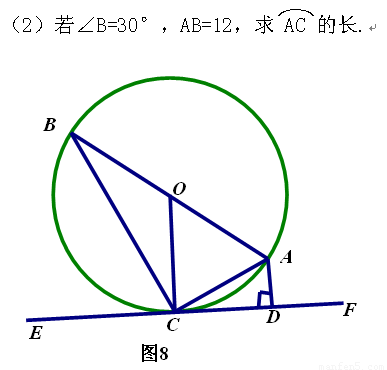
(2011年青海,25,7分)已知:如图8,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
(1)求证:∠BAC=∠CAD
【答案】
证法一:连接OC
∵ EF是过点C的⊙O的切线。
∴ OC⊥EF 又AD⊥EF
∴ OC∥AD
∴ ∠OCA=∠CAD
又∵OA=OC
∴ ∠OCA=∠BAC
∴∠BAC=∠CAD
证法二:连接OC
∵ EF是过点C的⊙O的切线。
∴ OC⊥EF
∴∠OCA+∠ACD=90°
∵ AD⊥EF
∴ ∠CAD+∠ACD=90°
∴ ∠OCA=∠CAD
∵ OA=OC ,∴∠OCA=∠BAC
∴ ∠BAC=∠CAD
(2)∵ ∠B=30° ∴∠AOC=60°
∵AB=12 ∴ 

【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 精美的轴对称图形,请你用所给出的几何图形:○○△
精美的轴对称图形,请你用所给出的几何图形:○○△ △ (两个圆,两个等边三角形,两条线段)为构件,构思一个独特,有意义的轴对称图形,并写上一句简要的解说词。
△ (两个圆,两个等边三角形,两条线段)为构件,构思一个独特,有意义的轴对称图形,并写上一句简要的解说词。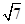 ,π和
,π和 这四个实数中,无理数是( )
这四个实数中,无理数是( )
 中,自变量x的取值范围是
。
中,自变量x的取值范围是
。