题目内容
 如图,靠一面20米的墙,用60米长的篱笆围成一个矩形场地.
如图,靠一面20米的墙,用60米长的篱笆围成一个矩形场地.(1)怎样围才能使矩形场地的面积为400平方米?
(2)能否使所围的矩形场地面积为810平方米,为什么?
分析:(1)设和墙平行的篱笆的长度是x米,根据利用一面墙,墙的长度为20m,用60m长的篱笆围一个矩形场地面积为400平方米,从而可列方程求解.
(2)设和墙平行的篱笆的长度是y米,根据面积为810平方米列方程求解,看求出的y即可作出判断.
(2)设和墙平行的篱笆的长度是y米,根据面积为810平方米列方程求解,看求出的y即可作出判断.
解答:解:(1)设和墙平行的篱笆的长度是x米,
故
(60-x)x=400,
x1=20,x2=40>20(舍去).
答:矩形的宽是20米,长是20米.
(2)设和墙平行的篱笆的长度是y米,
(60-y)y=810,
y2-60y+1620=0
△=4900-4×1620<0,
所以方程无解.
故不能围成面积为810平方米的场地.
故
| 1 |
| 2 |
x1=20,x2=40>20(舍去).
答:矩形的宽是20米,长是20米.
(2)设和墙平行的篱笆的长度是y米,
| 1 |
| 2 |
y2-60y+1620=0
△=4900-4×1620<0,
所以方程无解.
故不能围成面积为810平方米的场地.
点评:此题主要考查了一元二次方程的应用以及矩形的性质,解答此题要注意以下问题:
(1)矩形的一边为墙,且墙的长度不超过20米;
(2)根据矩形的面积公式列一元二次方程并根据根的判别式来判断是否两边长相等.
(1)矩形的一边为墙,且墙的长度不超过20米;
(2)根据矩形的面积公式列一元二次方程并根据根的判别式来判断是否两边长相等.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 14、用长为20米的篱笆,一面靠墙(墙的长度是10米),围成一个长方形花圃,如图,设AB边的长为x米,花圃的面积为y平方米,写出y与x的函数关系式及函数的定义域
14、用长为20米的篱笆,一面靠墙(墙的长度是10米),围成一个长方形花圃,如图,设AB边的长为x米,花圃的面积为y平方米,写出y与x的函数关系式及函数的定义域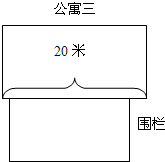 今年,我校准备新建学生“公寓四”,想利用“公寓三”一面长20米的墙,用木栏围出一片长方形的安全地带(如图所示),安全区一边靠着建筑物,现有木栏长40米.
今年,我校准备新建学生“公寓四”,想利用“公寓三”一面长20米的墙,用木栏围出一片长方形的安全地带(如图所示),安全区一边靠着建筑物,现有木栏长40米. 如图,靠一面20米的墙,用60米长的篱笆围成一个矩形场地.
如图,靠一面20米的墙,用60米长的篱笆围成一个矩形场地.