题目内容
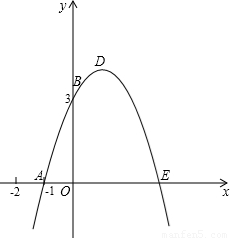
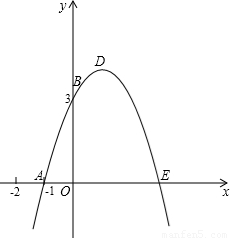
(2008•宜宾)已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.(1)求该抛物线的解析式;
(2)若该抛物线与x轴的另一个交点为E.求四边形ABDE的面积;
(3)△AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
(注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为
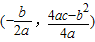 )
)
【答案】分析:(1)由于抛物线的解析式中只有两个未知数,因此可根据A,B两点的坐标,用待定系数法求出抛物线的解析式.
(2)由于四边形ABDE不是规则的四边形,因此可将ABDE分割成几个规则的图形后再进行求解.可设抛物线的对称轴与x轴的交点为F,那么四边形ABDE的面积=三角形AOB的面积+直角梯形BOFD的面积+三角形DFE的面积,根据抛物线的解析式可求得D、E两点的坐标,因此就可求出DF、OF、EF的长,根据A、B两点的坐标可得出OA、OB的长,那么求这些图形面积的相关线段的长就都已求出,进而可得出四边形ABDE的面积.
(3)可先根据B、D、E的坐标,求出BD、DE、BE的长,由于三角形AOB是直角三角形,要想判定两三角形是否相似,就要先判断三角形BDE是否为直角三角形,可根据BD、DE、BE三边的长以及勾股定理,来判断出三角形BDE是否为直角三角形,如果是直角三角形,那么找出三角形BDE中的直角,然后看夹直角的两组对应边是否成比例即可得出两三角形是否相似.
解答: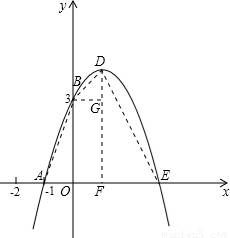 解:(1)由已知得:
解:(1)由已知得: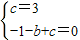
解得c=3,b=2
∴抛物线的线的解析式为y=-x2+2x+3.
(2)由顶点坐标公式得顶点坐标为(1,4)
所以对称轴为x=1,A,E关于x=1对称,
所以E(3,0)
设对称轴与x轴的交点为F
所以四边形ABDE的面积=S△ABO+S梯形BOFD+S△DFE= AO•BO+
AO•BO+ (BO+DF)•OF+
(BO+DF)•OF+ EF•DF
EF•DF
= ×1×3+
×1×3+ (3+4)×1+
(3+4)×1+ ×2×4
×2×4
=9
(3)相似.如图,连接AB、BD、DE,过点D作DF⊥x轴于点F,过点B作BG⊥DF于点G.
BD=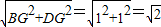
BE=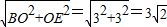
DE=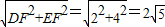
所以DE2=20,即:BD2+BE2=DE2,
所以△BDE是直角三角形,所以∠AOB=∠DBE=90°,且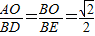 ,
,
所以△AOB∽△DEB.
点评:本题主要考查了用待定系数法求二次函数的解析式的方法,相似三角形的判定以及二次函数的综合应用等知识点.本题中确定二次函数的解析式是解题的关键.
(2)由于四边形ABDE不是规则的四边形,因此可将ABDE分割成几个规则的图形后再进行求解.可设抛物线的对称轴与x轴的交点为F,那么四边形ABDE的面积=三角形AOB的面积+直角梯形BOFD的面积+三角形DFE的面积,根据抛物线的解析式可求得D、E两点的坐标,因此就可求出DF、OF、EF的长,根据A、B两点的坐标可得出OA、OB的长,那么求这些图形面积的相关线段的长就都已求出,进而可得出四边形ABDE的面积.
(3)可先根据B、D、E的坐标,求出BD、DE、BE的长,由于三角形AOB是直角三角形,要想判定两三角形是否相似,就要先判断三角形BDE是否为直角三角形,可根据BD、DE、BE三边的长以及勾股定理,来判断出三角形BDE是否为直角三角形,如果是直角三角形,那么找出三角形BDE中的直角,然后看夹直角的两组对应边是否成比例即可得出两三角形是否相似.
解答:
 解:(1)由已知得:
解:(1)由已知得: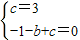
解得c=3,b=2
∴抛物线的线的解析式为y=-x2+2x+3.
(2)由顶点坐标公式得顶点坐标为(1,4)
所以对称轴为x=1,A,E关于x=1对称,
所以E(3,0)
设对称轴与x轴的交点为F
所以四边形ABDE的面积=S△ABO+S梯形BOFD+S△DFE=
 AO•BO+
AO•BO+ (BO+DF)•OF+
(BO+DF)•OF+ EF•DF
EF•DF=
 ×1×3+
×1×3+ (3+4)×1+
(3+4)×1+ ×2×4
×2×4=9
(3)相似.如图,连接AB、BD、DE,过点D作DF⊥x轴于点F,过点B作BG⊥DF于点G.
BD=
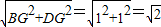
BE=
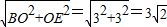
DE=
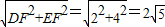
所以DE2=20,即:BD2+BE2=DE2,
所以△BDE是直角三角形,所以∠AOB=∠DBE=90°,且
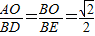 ,
,所以△AOB∽△DEB.
点评:本题主要考查了用待定系数法求二次函数的解析式的方法,相似三角形的判定以及二次函数的综合应用等知识点.本题中确定二次函数的解析式是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
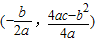 )
)
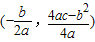 )
)
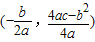 )
)