题目内容
有若干个数,按顺序记为a1,a2,a3,a4,…,若a1=-
,规定从第二个数起,每个数都等于“1与它前面的那个数的差的倒数”,试计算:a2=
,a3=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
3
3
,a2005=-
| 1 |
| 2 |
-
.| 1 |
| 2 |
分析:根据差倒数的定义列式求解即可得到a2、a3,a4,便不难发现,每三个数为一个循环组依次循环,用2005除以3,根据余数的情况确定与a2005相同数,即可得解.
解答:解:(1)a2=
=
,
a3=
=3,
a4=
=-
,
∵2005÷3=668余1,
∴a2005与a1相同,是-
.
故答案为:
;3;-
.
| 1 | ||
1-(-
|
| 2 |
| 3 |
a3=
| 1 | ||
1-
|
a4=
| 1 |
| 1-3 |
| 1 |
| 2 |
∵2005÷3=668余1,
∴a2005与a1相同,是-
| 1 |
| 2 |
故答案为:
| 2 |
| 3 |
| 1 |
| 2 |
点评:本题是对数字变化规律的考查,读懂题目信息,理解差倒数的定义并判断出每三个数为一个循环组依次循环是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
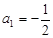 ,规定从第二个数起,每个数都等于“1与它前面的那个数的差的倒数”,试计算:a2= ,a3= ,a2005= .
,规定从第二个数起,每个数都等于“1与它前面的那个数的差的倒数”,试计算:a2= ,a3= ,a2005= .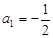 ,规定从第二个数起,每个数都等于“1与它前面的那个数的差的倒数”,试计算:a2= ,a3= ,a2005=
.
,规定从第二个数起,每个数都等于“1与它前面的那个数的差的倒数”,试计算:a2= ,a3= ,a2005=
.