题目内容
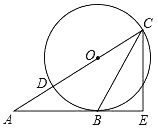
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 外接圆的圆心,过点
外接圆的圆心,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的切线,交
的切线,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
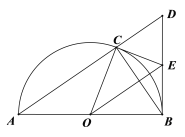
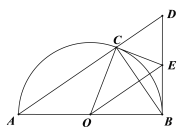
(1)求证:![]() ;
;
(2)填空:①当![]() 的度数为_________时,四边形
的度数为_________时,四边形![]() 为平行四边形;
为平行四边形;
②当![]() 时,
时,![]() 的值为____________.
的值为____________.
【答案】(1)详见解析;(2)①45°;②3.
【解析】
(1)先根据HL证明![]() ,得
,得![]() ,再根据等腰三角形三线合一的性质得出
,再根据等腰三角形三线合一的性质得出![]() ,而已知
,而已知![]() ,问题即得解决;
,问题即得解决;
(2)①由四边形![]() 为平行四边形可得CO∥BD,所以CO⊥BD,进一步即可求出∠A的度数;②由
为平行四边形可得CO∥BD,所以CO⊥BD,进一步即可求出∠A的度数;②由![]() 可得
可得![]() ,然后根据(1)的结论及OA=OB可得
,然后根据(1)的结论及OA=OB可得![]() ,
,
设BE=x,再得出AC与BE的关系即可求出结果.
(1)证明:∵![]() 是
是![]() 的切线,
的切线,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
(2)①若四边形![]() 为平行四边形,
为平行四边形,
则CO∥BD.
∵![]() ,
,
∴CO⊥AB,
∵OA=OC,
∴∠A=∠ACO=45°,
所以当![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.
故答案为45°.
②∵![]() ,∴
,∴![]() ,
,![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() .
.
设BE=x,则BD=2x,AD=4x,
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
故答案为3.

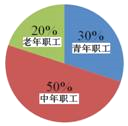
【题目】某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.
为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
年龄 | 26 | 42 | 57 |
健康指数 | 97 | 79 | 72 |
表2:小王抽样调查单位10名职工的健康指数
年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
表3:小李抽样调查单位10名职工的健康指数
年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
根据上述材料回答问题:
小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.