题目内容
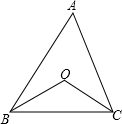 已知如图△ABC中,∠ABC和∠ACB的平分线BO和CO相交于O点
已知如图△ABC中,∠ABC和∠ACB的平分线BO和CO相交于O点(1)当∠A=40°时,∠BOC=
(2)当∠BOC=m时,则∠A为多少?(用含m的式子表示)说明理由.
分析:(1)△ABC中,已知∠A即可得到∠ABC与∠ACB的和,而BO、CO是∠ABC,∠ACB的两条角平分线,即可求得∠OBC与∠OCB的度数,根据三角形的内角和定理即可求解.
(2)根据三角形的内角和定理以及角平分线的定义和三角形外角和定理进行证明.
(2)根据三角形的内角和定理以及角平分线的定义和三角形外角和定理进行证明.
解答:解:(1)△ABC中,∠ABC+∠ACB=180°-∠A=180°-40°=140°,
∵BO、CO是∠ABC,∠ACB的两条角平分线.
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=70°,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=110°.
故答案为:110°;
(2)∠BOC=90°+
∠A.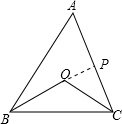
理由如下:延长BO交AC于点P,
∵BO、CO分别是∠ABC、∠ACB的平分线,
∴∠A+2∠ABP+2∠ACO=180°,
∴∠ABP+∠ACO=90°-
∠A,
∵∠BPC=∠A+∠ABP,
∠BOC=∠BPC+∠ACO,
∴∠BOC=∠A+∠ABP+∠ACO=90°+
∠A.
∵BO、CO是∠ABC,∠ACB的两条角平分线.
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC+∠OCB=
| 1 |
| 2 |
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=110°.
故答案为:110°;
(2)∠BOC=90°+
| 1 |
| 2 |

理由如下:延长BO交AC于点P,
∵BO、CO分别是∠ABC、∠ACB的平分线,
∴∠A+2∠ABP+2∠ACO=180°,
∴∠ABP+∠ACO=90°-
| 1 |
| 2 |
∵∠BPC=∠A+∠ABP,
∠BOC=∠BPC+∠ACO,
∴∠BOC=∠A+∠ABP+∠ACO=90°+
| 1 |
| 2 |
点评:此题主要考查了三角形的内角和定理,以及三角形的角平分线的定义,熟练应用三角形外角和定理得出是解决问题的关键.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 已知如图△ABC中,∠ABC=70°,∠ACB=50°,H是两条高CD、BE的交点,求∠DHE的度数.
已知如图△ABC中,∠ABC=70°,∠ACB=50°,H是两条高CD、BE的交点,求∠DHE的度数.

