题目内容
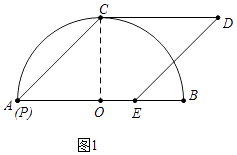
【题目】已知:如图,选段AB=4,以AB为直径作半圆O,点C为弧AB的中点,点P为直径AB上一点,联结PC,过点C作CD∥AB,且CD=PC,过点D作DE∥PC,交射线PB于点E,PD与CE相交于点Q. 
(1)若点P与点A重合,求BE的长;
(2)设PC=x, ![]() =y,当点P在线段AO上时,求y与x的函数关系式及定义域;
=y,当点P在线段AO上时,求y与x的函数关系式及定义域;
(3)当点Q在半圆O上时,求PC的长.
【答案】
(1)解:如图1中,连接OC.
∵ ![]() =
= ![]() ,
,
∴CO⊥AB,△AOC是等腰直角三角形,AC= ![]() OC=2
OC=2 ![]() ,
,
∵四边形ACDE是菱形,
∴AE=AC=2 ![]() ,
,
∴BE=AB﹣AE=4﹣2 ![]()
(2)解:如图2中,
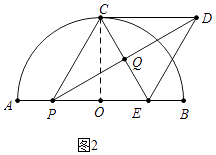
∵PC=x,OC=2,
∴OP= ![]() ,OE=x﹣
,OE=x﹣ ![]() ,
,
∵四边形PCDE是菱形,
∴PD⊥EC,CQ=QE,PQ=QD,
∵ ![]() =
= ![]() =y,
=y,
∴tan∠PEQ= ![]() =
= ![]() ,
,
∴y= ![]() (2≤x≤2
(2≤x≤2 ![]() )
)
(3)解:如图3中,
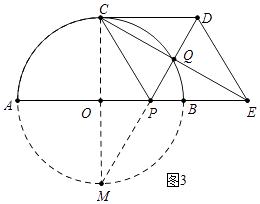
∵点Q在⊙O上,∠CQP=90°,
∴∠CQP所以对的弦CM是直径,
∵∠M+∠OPM=90°,∠QPE+∠QEP=90°,∠OPM=∠QPE,
∴∠M=∠QEP,易知∠PCM=∠M,∠PCQ=∠PEQ,
∴∠PCO=∠PCQ=∠CEO=30°,
在Rt△POC中,PC=OC÷cos30°= ![]()
【解析】(1)如图1中,连接OC.只要证明△AOC是等腰直角三角形即可.(2)由PC=x,OC=2,可得OP= ![]() ,OE=x﹣
,OE=x﹣ ![]() ,由四边形PCDE是菱形,推出PD⊥EC,CQ=QE,PQ=QD,由
,由四边形PCDE是菱形,推出PD⊥EC,CQ=QE,PQ=QD,由 ![]() =
= ![]() =y,推出tan∠PEQ=
=y,推出tan∠PEQ= ![]() =
= ![]() ,由此即可解决问题.(3)由点Q在⊙O上,∠CQP=90°,推出∠CQP所以对的弦CM是直径,由∠M+∠OPM=90°,∠QPE+∠QEP=90°,∠OPM=∠QPE,推出∠M=∠QEP,易知∠PCM=∠M,∠PCQ=∠PEQ,推出∠PCO=∠PCQ=∠CEO=30°,由此即可解决问题.
,由此即可解决问题.(3)由点Q在⊙O上,∠CQP=90°,推出∠CQP所以对的弦CM是直径,由∠M+∠OPM=90°,∠QPE+∠QEP=90°,∠OPM=∠QPE,推出∠M=∠QEP,易知∠PCM=∠M,∠PCQ=∠PEQ,推出∠PCO=∠PCQ=∠CEO=30°,由此即可解决问题.

 阅读快车系列答案
阅读快车系列答案