题目内容
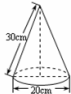
 如图是小明制作的一个圆锥形纸帽的示意图,围成这个纸帽的纸(圆锥的侧面)的面积为
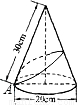
如图是小明制作的一个圆锥形纸帽的示意图,围成这个纸帽的纸(圆锥的侧面)的面积为分析:易得圆锥的底面半径为10cm,圆锥的侧面积=π×底面半径×母线长;易得圆锥的底面周长,也就是侧面展开图的弧长,利用弧长公式可得圆锥侧面展开图的圆心角度数,求得侧面展开图中AA′的距离即为最短的红线长.
解答: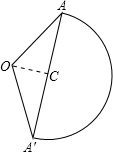 解:∵圆锥的底面半径为20÷2=10cm,
解:∵圆锥的底面半径为20÷2=10cm,
∴圆锥的侧面积=π×10×30=300πcm2.圆锥的底面周长为2π×10=20πcm.
设圆锥侧面展开图的圆心角为n,
=20π,
解得n=120°.
作OC⊥AA′于点C,
∴∠AOC=60°,
∴AC=AO×sin∠AOC=15
cm,
∴AA′=2AC=30
cm.
故答案为300π;30
.
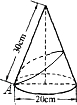
 解:∵圆锥的底面半径为20÷2=10cm,
解:∵圆锥的底面半径为20÷2=10cm,∴圆锥的侧面积=π×10×30=300πcm2.圆锥的底面周长为2π×10=20πcm.
设圆锥侧面展开图的圆心角为n,
| nπ×30 |
| 180 |
解得n=120°.
作OC⊥AA′于点C,
∴∠AOC=60°,
∴AC=AO×sin∠AOC=15
| 3 |
∴AA′=2AC=30
| 3 |
故答案为300π;30
| 3 |
点评:考查圆锥的计算;突破点是求得圆锥侧面展开图的圆心角度数;用到的知识点为:立体几何中的最短距离问题要转换为平面几何中求两点的距离问题;圆锥的底面周长等于侧面展开图的弧长.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
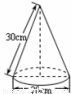
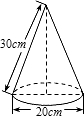 如图是小明制作的一个圆锥形纸帽的示意图.围成这个纸帽的纸的面积为
如图是小明制作的一个圆锥形纸帽的示意图.围成这个纸帽的纸的面积为