ΧβΡΩΡΎ»ί
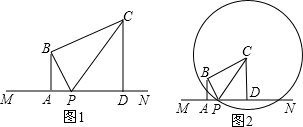
Θ®2013•“Υ–Υ –“ΜΡΘΘ©»γΆΦ1Θ§BAΓΆMNΘ§¥ΙΉψΈΣAΘ§BA=4Θ§ΒψP «…δœΏAN…œΒΡ“ΜΗωΕ·ΒψΘ®ΒψP”κΒψA≤Μ÷ΊΚœΘ©Θ§ΓœBPC=ΓœBPAΘ§BCΓΆBPΘ§ΙΐΒψCΉςCDΓΆMNΘ§¥ΙΉψΈΣDΘ§…ηAP=xΘ°
Θ®1Θ©CDΒΡ≥ΛΕ» «ΖώΥφΉ≈xΒΡ±δΜ·Εχ±δΜ·ΘΩ»τ±δΜ·Θ§«κ”ΟΚ§xΒΡ¥ζ ΐ Ϋ±μ ΨCDΒΡ≥ΛΕ»ΘΜ»τ≤Μ±δΜ·Θ§«κ«σ≥ωœΏΕΈCDΒΡ≥ΛΕ»Θ°
Θ®2Θ©ΓςPBCΒΡΟφΜΐ «Ζώ¥φ‘ΎΉν–Γ÷ΒΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ω’βΗωΉν–Γ÷ΒΘ§≤Δ«σ≥ω¥Υ ±ΒΡxΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
Θ®3Θ©Β±x»ΓΚΈ÷Β ±Θ§ΓςABPΚΆΓςCDPœύΥΤΘ°
Θ®4Θ©»γΆΦ2Θ§Β±“‘CΈΣ‘≤–ΡΘ§“‘CPΈΣΑκΨΕΒΡ‘≤”κœΏΕΈAB”–ΙΪΙ≤Βψ ±Θ§«σxΒΡ÷ΒΘ°
Θ®1Θ©CDΒΡ≥ΛΕ» «ΖώΥφΉ≈xΒΡ±δΜ·Εχ±δΜ·ΘΩ»τ±δΜ·Θ§«κ”ΟΚ§xΒΡ¥ζ ΐ Ϋ±μ ΨCDΒΡ≥ΛΕ»ΘΜ»τ≤Μ±δΜ·Θ§«κ«σ≥ωœΏΕΈCDΒΡ≥ΛΕ»Θ°
Θ®2Θ©ΓςPBCΒΡΟφΜΐ «Ζώ¥φ‘ΎΉν–Γ÷ΒΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ω’βΗωΉν–Γ÷ΒΘ§≤Δ«σ≥ω¥Υ ±ΒΡxΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
Θ®3Θ©Β±x»ΓΚΈ÷Β ±Θ§ΓςABPΚΆΓςCDPœύΥΤΘ°
Θ®4Θ©»γΆΦ2Θ§Β±“‘CΈΣ‘≤–ΡΘ§“‘CPΈΣΑκΨΕΒΡ‘≤”κœΏΕΈAB”–ΙΪΙ≤Βψ ±Θ§«σxΒΡ÷ΒΘ°

Ζ÷ΈωΘΚΘ®1Θ©»γΆΦ1Θ§―”≥ΛCBΚΆPAΘ§Φ«ΫΜΒψΈΣΒψQΘ°ΗυΨίΒ»―ϋΓςQPCΓΑ»ΐΚœ“ΜΓ±ΒΡ–‘÷ ÷ΛΒΟQB=BCΘΜ”…œύΥΤ»ΐΫ«–ΈΘ®ΓςQABΓΉΓςQDCΘ©ΒΡΕ‘”Π±Ώ≥…±»άΐΒΟΒΫ
=
=
Θ§‘ρCD=2ABΘΜ
Θ®2Θ©»γΆΦ2Θ§ΙΐΒψBΉςBFΓΆPCΘ§¥ΙΉψΈΣFΘ°÷ΛBF=BA=4Θ°“ρΈΣCPΓίCDΘ§Υυ“‘CPΉν–Γ÷ΒΈΣ8Θ§ΒΟ≥ωΓςPBCΟφΜΐΒΡΉν–Γ÷ΒΘ§¥Υ ±ΓςBAP «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§AP=AB=4Θ§ΫχΕχΒΟ≥ω¥πΑΗΘΜ
Θ®3Θ©Β±ΓςBAPΓΉΓςCDP ±Θ§“ΉΒΟΓœBPA=60ΓψΘ§x=AP=
=
Θ§Β±ΓςBAPΓΉΓςPDC ±Θ§“ΉΒΟΓœBPA=30ΓψΘ§AP=
=4
Θ§«σ≥ωxΒΡ÷ΒΦ¥Ω…ΘΜ
Θ®4Θ©ΗυΨίΒ±ΒψA‘ΎΓ―C…œ ±Θ§”…Θ®1Θ©ΦΑ¥ΙΨΕΕ®άμΒΟΘΚAE=AD=DP=
xΘ§ΫχΕχΒΟ≥ωxΒΡ»Γ÷ΒΖΕΈßΘ°
| AB |
| CD |
| QB |
| QC |
| 1 |
| 2 |
Θ®2Θ©»γΆΦ2Θ§ΙΐΒψBΉςBFΓΆPCΘ§¥ΙΉψΈΣFΘ°÷ΛBF=BA=4Θ°“ρΈΣCPΓίCDΘ§Υυ“‘CPΉν–Γ÷ΒΈΣ8Θ§ΒΟ≥ωΓςPBCΟφΜΐΒΡΉν–Γ÷ΒΘ§¥Υ ±ΓςBAP «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§AP=AB=4Θ§ΫχΕχΒΟ≥ω¥πΑΗΘΜ
Θ®3Θ©Β±ΓςBAPΓΉΓςCDP ±Θ§“ΉΒΟΓœBPA=60ΓψΘ§x=AP=
| BA |
| tan60Γψ |
4
| ||
| 3 |
| BA |
| tan300 |
| 3 |
Θ®4Θ©ΗυΨίΒ±ΒψA‘ΎΓ―C…œ ±Θ§”…Θ®1Θ©ΦΑ¥ΙΨΕΕ®άμΒΟΘΚAE=AD=DP=
| 1 |
| 2 |
Ϋβ¥πΘΚ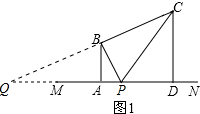 ΫβΘΚΘ®1Θ©CDΒΡ≥ΛΕ»≤Μ±δΜ·Θ°
ΫβΘΚΘ®1Θ©CDΒΡ≥ΛΕ»≤Μ±δΜ·Θ°
άμ”…»γœ¬ΘΚ
»γΆΦ1Θ§―”≥ΛCBΚΆPAΘ§Φ«ΫΜΒψΈΣΒψQΘ°
ΓΏΓœBPC=ΓœBPAΘ§BCΓΆBPΘ§
ΓύQB=BCΘ®Β»―ϋ»ΐΫ«–ΈΓΑ»ΐΚœ“ΜΓ±ΒΡ–‘÷ Θ©Θ°
ÿBAâMNȧCDâMNȧ
ΓύABΓΈCDΘ§
ΓύΓςQABΓΉΓςQDCΘ§
Γύ
=
=
ΓύCD=2AB=2ΓΝ4=8Θ§
Φ¥CD=8
Θ®2Θ©»γΆΦ2Θ§ΙΐΒψBΉςBFΓΆPCΘ§¥ΙΉψΈΣFΘ°
ΓΏΓœBPC=ΓœBPAΘ§BAΓΆMNΘ§
ΓύBF=BA=4Θ°
ΓΏCPΓίCDΘ§ΓύCPΓί8Θ§Φ¥CPΉν–Γ÷ΒΈΣ8Θ§
ΓύΓςPBCΟφΜΐΒΡΉν–Γ÷Β=
ΓΝ8ΓΝ4=16Θ§
¥Υ ±ΓςBAP «Β»―ϋ»ΐΫ«–ΈΘ§AP=AB=4Θ§Φ¥x=4ΘΜ
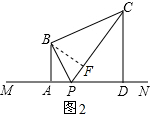
Θ®3Θ©Β±ΓςBAPΓΉΓςCDP ±Θ§
ΓΏΓœBPC=ΓœBPAΘ§ΓœCPD=ΓœBPAΘ§
ΓύΓœBPA=ΓœBPC=ΓœCPD=60ΓψΘ§
ΓύAP=
=
Θ§
Φ¥x=
Θ§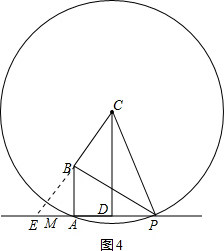
»γΆΦ3Θ§Β±ΓςBAPΓΉΓςPDC ±Θ§
ΓΏΓœCPB=ΓœBPAΘ§ΓœPCD=ΓœBPAΘ§
Γύ3ΓœBPA=90ΓψΘ§
ΓύΓœBPA=30ΓψΘ§
ΓύAP=
=4
Θ§
Φ¥x=4
Θ§
Υυ“‘Β±x=
Μρ4
±Θ§ΓςABPΚΆΓςCDPœύΥΤΘΜ
Θ®4Θ©»γΆΦ4Θ§―”≥ΛCBΚΆPAœύΫΜ”ΎΒψEΘ§
Β±ΒψA‘ΎΓ―C…œ ±Θ§”…Θ®1Θ©ΦΑ¥ΙΨΕΕ®άμΒΟΘΚ
AE=AD=DP=
xȧ
”…ΓςABEΓΉΓςAPBΒΟΘ§AB2=AE•APΘ§
Υυ“‘
x2=16Θ§Φ¥x=4
Θ§
Υυ“‘xΒΡ»Γ÷ΒΖΕΈß «0ΘΦxΓή4
Θ°
 ΫβΘΚΘ®1Θ©CDΒΡ≥ΛΕ»≤Μ±δΜ·Θ°
ΫβΘΚΘ®1Θ©CDΒΡ≥ΛΕ»≤Μ±δΜ·Θ°άμ”…»γœ¬ΘΚ
»γΆΦ1Θ§―”≥ΛCBΚΆPAΘ§Φ«ΫΜΒψΈΣΒψQΘ°
ΓΏΓœBPC=ΓœBPAΘ§BCΓΆBPΘ§
ΓύQB=BCΘ®Β»―ϋ»ΐΫ«–ΈΓΑ»ΐΚœ“ΜΓ±ΒΡ–‘÷ Θ©Θ°
ÿBAâMNȧCDâMNȧ
ΓύABΓΈCDΘ§
ΓύΓςQABΓΉΓςQDCΘ§
Γύ
| AB |
| CD |
| QB |
| QC |
| 1 |
| 2 |

ΓύCD=2AB=2ΓΝ4=8Θ§
Φ¥CD=8
Θ®2Θ©»γΆΦ2Θ§ΙΐΒψBΉςBFΓΆPCΘ§¥ΙΉψΈΣFΘ°
ΓΏΓœBPC=ΓœBPAΘ§BAΓΆMNΘ§
ΓύBF=BA=4Θ°
ΓΏCPΓίCDΘ§ΓύCPΓί8Θ§Φ¥CPΉν–Γ÷ΒΈΣ8Θ§

ΓύΓςPBCΟφΜΐΒΡΉν–Γ÷Β=
| 1 |
| 2 |
¥Υ ±ΓςBAP «Β»―ϋ»ΐΫ«–ΈΘ§AP=AB=4Θ§Φ¥x=4ΘΜ
Θ®3Θ©Β±ΓςBAPΓΉΓςCDP ±Θ§
ΓΏΓœBPC=ΓœBPAΘ§ΓœCPD=ΓœBPAΘ§
ΓύΓœBPA=ΓœBPC=ΓœCPD=60ΓψΘ§
ΓύAP=
| BA |
| tan60Γψ |
4
| ||
| 3 |
Φ¥x=
4
| ||
| 3 |
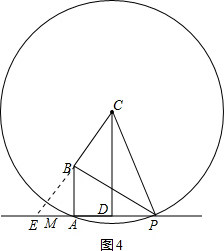
»γΆΦ3Θ§Β±ΓςBAPΓΉΓςPDC ±Θ§
ΓΏΓœCPB=ΓœBPAΘ§ΓœPCD=ΓœBPAΘ§
Γύ3ΓœBPA=90ΓψΘ§
ΓύΓœBPA=30ΓψΘ§
ΓύAP=
| BA |
| tan300 |
| 3 |
Φ¥x=4
| 3 |
Υυ“‘Β±x=
4
| ||
| 3 |
| 3 |
Θ®4Θ©»γΆΦ4Θ§―”≥ΛCBΚΆPAœύΫΜ”ΎΒψEΘ§
Β±ΒψA‘ΎΓ―C…œ ±Θ§”…Θ®1Θ©ΦΑ¥ΙΨΕΕ®άμΒΟΘΚ
AE=AD=DP=
| 1 |
| 2 |
”…ΓςABEΓΉΓςAPBΒΟΘ§AB2=AE•APΘ§
Υυ“‘
| 1 |
| 2 |
| 2 |
Υυ“‘xΒΡ»Γ÷ΒΖΕΈß «0ΘΦxΓή4
| 2 |
ΒψΤάΘΚ¥ΥΧβ÷ς“ΣΩΦ≤ιΝΥ‘≤ΒΡΉέΚœ”Π”Ο“‘ΦΑœύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®”κ–‘÷ ΚΆ»ώΫ«»ΐΫ«Κ· ΐΙΊœΒΒ»÷Σ ΕΘ§ λΝΖάϊ”ΟœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΒΟ≥ωœΏΕΈ÷°ΦδΒΡΙΊœΒ «ΫβΧβΙΊΦϋΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 Ά§≤ΫΑ¬ ΐœΒΝ–¥πΑΗ
Ά§≤ΫΑ¬ ΐœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
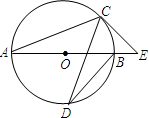 Θ®2013•“Υ–Υ –“ΜΡΘΘ©»γΆΦΘ§AB «Γ―OΒΡ÷±ΨΕΘ§CΓΔD «Γ―O…œΒΡΒψΘ§ΓœCDB=20ΓψΘ§ΙΐΒψCΉςΓ―OΒΡ«–œΏΫΜABΒΡ―”≥ΛœΏ”ΎΒψEΘ§‘ρΓœE=
Θ®2013•“Υ–Υ –“ΜΡΘΘ©»γΆΦΘ§AB «Γ―OΒΡ÷±ΨΕΘ§CΓΔD «Γ―O…œΒΡΒψΘ§ΓœCDB=20ΓψΘ§ΙΐΒψCΉςΓ―OΒΡ«–œΏΫΜABΒΡ―”≥ΛœΏ”ΎΒψEΘ§‘ρΓœE= Θ®2013•“Υ–Υ –“ΜΡΘΘ©»γΆΦΘ§‘ΎΓςABC÷–Θ§AC=BCΘΨABΘ§ΒψPΈΣΓςABCΥυ‘ΎΤΫΟφΡΎ“ΜΒψΘ§«“ΒψP”κΓςABCΒΡ»Έ“βΝΫΗωΕΞΒψΙΙ≥…ΓςPABΘ§ΓςPBCΘ§ΓςPACΨυ «Β»―ϋ»ΐΫ«–ΈΘ§‘ρ¬ζΉψ…œ ωΧθΦΰΒΡΥυ”–ΒψPΒΡΗω ΐΈΣ
Θ®2013•“Υ–Υ –“ΜΡΘΘ©»γΆΦΘ§‘ΎΓςABC÷–Θ§AC=BCΘΨABΘ§ΒψPΈΣΓςABCΥυ‘ΎΤΫΟφΡΎ“ΜΒψΘ§«“ΒψP”κΓςABCΒΡ»Έ“βΝΫΗωΕΞΒψΙΙ≥…ΓςPABΘ§ΓςPBCΘ§ΓςPACΨυ «Β»―ϋ»ΐΫ«–ΈΘ§‘ρ¬ζΉψ…œ ωΧθΦΰΒΡΥυ”–ΒψPΒΡΗω ΐΈΣ Θ®2013•“Υ–Υ –“ΜΡΘΘ©»γΆΦΘ§“―÷ΣΓςABC‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Τδ÷–ΒψAΓΔBΓΔC»ΐΒψΒΡΉχ±ξΖ÷±πΈΣΘ®1Θ§2
Θ®2013•“Υ–Υ –“ΜΡΘΘ©»γΆΦΘ§“―÷ΣΓςABC‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Τδ÷–ΒψAΓΔBΓΔC»ΐΒψΒΡΉχ±ξΖ÷±πΈΣΘ®1Θ§2