题目内容
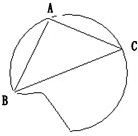 如图,要把破残的圆形模具复制完整,已知弧上的三点A、B、C;
如图,要把破残的圆形模具复制完整,已知弧上的三点A、B、C;(1)用尺规作图法,找出B、A、C所在圆的圆心(保留作图痕迹,不写作法)
(2)若△ABC是等腰直角三角形,腰AB=5cm,求圆形模具中弧AC的长.
分析:(1)根据垂径定理,作线段AB的垂直平分线DM,作AC的垂直平分线EN,DM、EN交点必为圆心O;
(2)连接AO.根据AB=AC,AO过圆心,依据垂径定理推论,根据勾股定理求半径,即可得出答案.
(2)连接AO.根据AB=AC,AO过圆心,依据垂径定理推论,根据勾股定理求半径,即可得出答案.
解答:解:(1)如图所示:
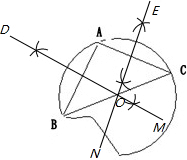
(2)连接AO,
∵△ABC是等腰直角三角形,腰AB=5cm,
∴AC=5,
BC=
=5
,
∴AO⊥BC,
∴∠AOC=90°,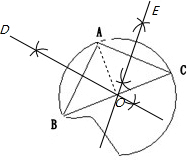
∴圆的半径为:
,
∴弧AC的长为:
=
π.

(2)连接AO,
∵△ABC是等腰直角三角形,腰AB=5cm,
∴AC=5,
BC=
| 52+52 |
| 2 |
∴AO⊥BC,
∴∠AOC=90°,

∴圆的半径为:
5
| ||
| 2 |
∴弧AC的长为:
90π×
| ||||
| 180 |
5
| ||
| 4 |
点评:此题主要考查了垂径定理的应用,是一道实际问题,将圆的相关知识和勾股定理结合,有一定的开放性,可以作出图形,根据勾股定理和垂径定理解答.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目