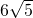题目内容
矩形的一条长边的中点与另一条长边构成等腰直角三角形,已知矩形的周长是36,则矩形一条对角线长是( )A.
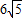
B.5
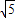
C.

D.3

【答案】分析:因为是等腰直角三角形,所以底角是45°,所以中点与矩形顶点的连线也是矩形直角的角平分线,即矩形被分成三个等腰直角三角形,因此矩形的长是宽的2倍.再根据周长即可求出长与宽,利用勾股定理就可以求出对角线的长.
解答: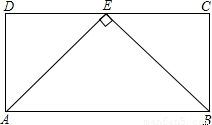 解:如图,∵△ABE是等腰直角三角形,
解:如图,∵△ABE是等腰直角三角形,
∴∠BAE=∠ABE=45°,
又矩形ABCD,∴∠DAE=∠90°-45°=45°,
∴Rt△ADE是等腰直角三角形,
∴AD=DE,
∵点E是中点,
∴CD=2AD,
又∵(AD+CD)×2=36,
∴AD=6,CD=12,
所以对角线的长=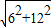 =6
=6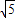 .
.
故选A.
点评:判断出矩形被分成三个等腰直角三角形,然后根据中点得出矩形的长是宽的2倍,是解题的关键.
解答:
 解:如图,∵△ABE是等腰直角三角形,
解:如图,∵△ABE是等腰直角三角形,∴∠BAE=∠ABE=45°,
又矩形ABCD,∴∠DAE=∠90°-45°=45°,
∴Rt△ADE是等腰直角三角形,
∴AD=DE,
∵点E是中点,
∴CD=2AD,
又∵(AD+CD)×2=36,
∴AD=6,CD=12,
所以对角线的长=
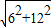 =6
=6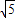 .
.故选A.
点评:判断出矩形被分成三个等腰直角三角形,然后根据中点得出矩形的长是宽的2倍,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
矩形的一条长边的中点与另一条长边构成等腰直角三角形,已知矩形的周长是36,则矩形一条对角线长是( )
A、6
| ||
B、5
| ||
C、4
| ||
D、3
|