题目内容
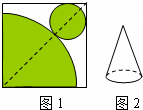
如图1，在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形，使之恰好围成图2所示的一个圆锥，则圆锥的高为（ ）A、
| ||
| B、4cm | ||
C、
| ||
D、
|
分析：利用已知得出底面圆的半径为：1，周长为2π，进而得出母线长，即可得出答案．
解答：解：∵半径为1cm的圆形，
∴底面圆的半径为：1，周长为2π，
扇形弧长为：2π=
，
∴R=4，即母线为4cm，
∴圆锥的高为：
=
（cm）．
故选：C．
∴底面圆的半径为：1，周长为2π，
扇形弧长为：2π=
| 90πR |
| 180 |
∴R=4，即母线为4cm，
∴圆锥的高为：
| 16-1 |
| 15 |
故选：C．
点评：此题主要考查了圆锥展开图与原图对应情况，以及勾股定理等知识，根据已知得出母线长是解决问题的关键．
练习册系列答案
相关题目
如图1，在正方形铁皮上剪下一个圆形和扇形，使之恰好围成图2所示的一个圆锥模型．设圆的半径为r，扇形半径为R，则圆的半径r与扇形半径R之间的关系为
如图1，在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形，使之恰好围成图2所示的一个圆锥，求圆锥的高．
如图(1)，在正方形铁皮上剪下一个圆形和扇形，使之恰好围成图(2)所示的一个圆锥模型，则圆的半径r与扇形的半径R之间的关系为 ( )
| A．R＝2r | B．R＝ r |
| C．R＝3r | D．R＝4r |
r