Question

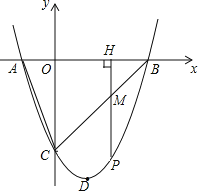
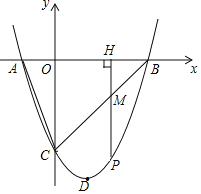
【题目】如图，抛物线y＝x2+bx+c与x轴相交于A、B两点，点A的坐标为(﹣1，0)，点B的坐标为(3，0)．

（1）求二次函数的解析式；

（2）求△ABC的面积；

（3）若P是第四象限内抛物线上任意一点，PH⊥x轴于点H，与BC交于点M．求线段PM的最大值．

Answer 1

【答案】（1）y＝x2﹣2x﹣3；（2）6；（3）

【解析】

（1）将点A、B的坐标代入抛物线表达式，然后解方程组求出b、c的值即可；

（2）根据抛物线解析式求得点C的坐标，易得线段OC，AB的长度，所以由三角形面积公式解答即可；

（3）根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得二次函数，根据二次函数的性质，可得答案．

（1）将A（﹣1，0），B（3，0）代入y＝x2+bx+c得，

，

解得，

∴抛物线解析式为y＝x2﹣2x﹣3；

（2）由A（﹣1，0），B（3，0）知，AB＝4．

∵抛物线解析式为y＝x2﹣2x﹣3，

∴C（0，﹣3），

∴OC＝3．

∴S△ABC＝ABOC＝×4×3＝6，即△ABC的面积是6；

（3）设BC的解析式为y＝kx+t，

将B，C的坐标代入函数解析式，得

，

解得 ,

∴BC的解析式为y＝x﹣3，

设M（n，n﹣3），P（n，n2﹣2n﹣3），

∴PM＝（n﹣3）﹣（n2﹣2n﹣3）＝﹣n2+3n＝﹣（n﹣）2+，

当n＝时，PM最大＝．