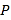题目内容
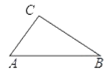
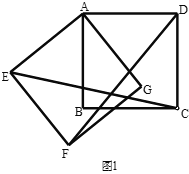
【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△ADE可以由△ABC绕点 A顺时针旋转90°得到,点D 与点B是对应点,点E与点C是对应点),连接CE,则∠CED的度数是_____.

【答案】15°.
【解析】
先根据旋转的性质得出AE=AC,∠DAE=∠BAC=90°,那么△CAE为等腰直角三角形,则∠CEA=45°.再根据直角三角形的两个锐角互求出∠BCA=30°,那么∠DEA=∠BCA=30°,那么根据∠CED=∠CEA-∠DEA即可求解.
∵△ADE可以由△ABC绕点A顺时针旋转90°得到,
∴△ADE≌△ABC,
∴AE=AC,∠DAE=∠BAC=90°,
∴△CAE为等腰直角三角形,则∠CEA=45°.
∵Rt△ABC中,∠BAC=90°,∠B=60°,
∴∠BCA=30°,
∴∠DEA=∠BCA=30°.
∴∠CED=∠CEA﹣∠DEA=45°﹣30°=15°.
故答案为:15°.

 小学夺冠AB卷系列答案
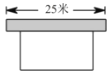
小学夺冠AB卷系列答案【题目】为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 | 乙 | 丙 | |
单价(元/棵) | 14 | 16 | 28 |
合理用地(m2/棵) | 0.4 | 1 | 0.4 |

【题目】某数学“综合与实践”小组的同学把“测量大桥斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表.
项目 | 内容 | ||
课题 | 测量斜拉索顶端到桥面的距离 | ||
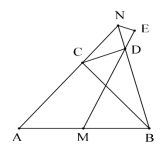
测量示意图 |
| 说明:大桥两侧一组斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内. | |
测量数据 | ∠A的度数 | ∠B的度数 | AB的长度 |
45° | 30° | 240米 | |
… | … | ||
请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离.(结果精确到0.1米)(参考数据:![]() =1.414,
=1.414,![]() =1.732)
=1.732)