题目内容
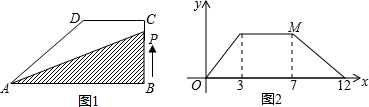
如图1,在直角梯形ABCD中,∠B=90°,DC∥AB,动点P从B点出发,沿梯形的边由B→C→D→A运动,设点P运动的路程为x,△ABP的面积为y,如果关于x的函数y的图象如图2所示,那么△ABC的面积为________.

16
分析:由图2可知;BC=4,DC=5,AD=5,过D作DE⊥AB于E,得到平行四边形DCBE,推出DC=BE=5,BC=DE=4,∠DEA=90°,由勾股定理求出AE,得到AB的长,根据三角形的面积公式即可求出答案.
解答: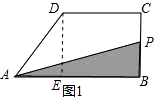 解:由图2可知;BC=4,DC=9-4=5,AD=14-9=5,
解:由图2可知;BC=4,DC=9-4=5,AD=14-9=5,
过D作DE⊥AB于E,
∵∠B=90°,
∴DE∥BC,
∵CD∥AB,
∴四边形DCBE是平行四边形,
∴DC=BE=5,BC=DE=4,∠DEA=90°,
由勾股定理得:AE=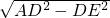 =3,
=3,
∴AB=3+5=8,
∴△ABC的面积是 AB•BC=
AB•BC= ×8×4=16,
×8×4=16,
故答案为:16.
点评:本题主要考查对直角梯形的性质,平行四边形的性质和判定,勾股定理,三角形的面积,动点问题与函数图象等知识点的理解和掌握,正确观察图形得到数据是解此题的关键.
分析:由图2可知;BC=4,DC=5,AD=5,过D作DE⊥AB于E,得到平行四边形DCBE,推出DC=BE=5,BC=DE=4,∠DEA=90°,由勾股定理求出AE,得到AB的长,根据三角形的面积公式即可求出答案.
解答:
 解:由图2可知;BC=4,DC=9-4=5,AD=14-9=5,
解:由图2可知;BC=4,DC=9-4=5,AD=14-9=5,过D作DE⊥AB于E,
∵∠B=90°,
∴DE∥BC,
∵CD∥AB,
∴四边形DCBE是平行四边形,
∴DC=BE=5,BC=DE=4,∠DEA=90°,
由勾股定理得:AE=
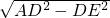 =3,
=3,∴AB=3+5=8,
∴△ABC的面积是
 AB•BC=
AB•BC= ×8×4=16,
×8×4=16,故答案为:16.
点评:本题主要考查对直角梯形的性质,平行四边形的性质和判定,勾股定理,三角形的面积,动点问题与函数图象等知识点的理解和掌握,正确观察图形得到数据是解此题的关键.

练习册系列答案
相关题目
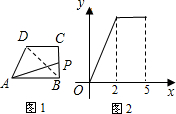 如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )| A、3 | B、4 | C、5 | D、6 |