题目内容
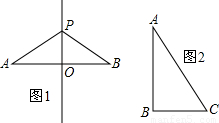
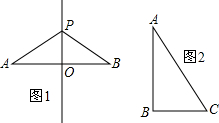
下列说法:(1)如图1,已知PA=PB,则PO是线段AB的垂直平分线;
(2)对于反比例函数
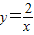 ,(x1,y1),(x2,y2)是其图象上两点,若x1<x2,则y1>y2;
,(x1,y1),(x2,y2)是其图象上两点,若x1<x2,则y1>y2; (3)对角线互相垂直平分的四边形是菱形;
(4)如图2,在△ABC中,∠A=30°,BC=2,则AC=4;
(5)一组对边平行的四边形是梯形;
(6)
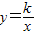 是反比例函数;
是反比例函数;(7)若一个等腰三角形的两边长为2和3,那么它的周长为7,
其中正确的有( )个.

A.0
B.1
C.2
D.5
【答案】分析:(1)根据垂直平分线的性质,垂直平分线上的点到线段两端点距离相等得出答案即可;
(2)根据反比例函数的性质得出,k>0,每个象限内,y随x的增大而减小,分别讨论得出答案;
(3)根据菱形的判定定理得出答案即可;
(4)根据直角三角形中30°所对的边等于斜边的一半,得出答案;
(5)根据梯形的定义得出,一组对边平行另一组对边不平行的四边形是梯形得出答案;
(6)根据反比例函数的定义得出答案;
(7)根据等腰三角形的性质得出答案.
解答:解:(1)根据垂直平分线的性质,P在AB垂直平分线上,但是O不一定在AB的垂直平分线上,
∴PO不一定是AB垂直平分线,故此选项错误;
(2)根据反比例函数的性质得出,
k>0,每一个象限内y随x的增大而减小,当x1<x2<0时,
∵x1<x2,∴y1>y2;
当0<x1<x2时,∵x1<x2,∴y1>y2;
当x1<0,x2>0,(x1,y1)在第三象限,(x2,y2)在第一象限,
∴y2>y1.故此选项错误;
(3)根据菱形的判定定理得出,对角线互相垂直平分的四边形是菱形,故此选项正确;
(4)根据只有直角三角形中30°所对的边等于斜边的一半,而此三角形不一定是直角三角形,
则AC不一定等于4,故此选项错误;
(5)根据梯形的定义得出,一组对边平行另一组对边不平行的四边形是梯形,故此选项错误;
(6)根据反比例函数的定义, 是反比例函数,应该k≠0,故此选项错误;
是反比例函数,应该k≠0,故此选项错误;
(7)若一个等腰三角形的两边长为2和3,那么它的周长为7,也可能是3+3+2=8,故此选项错误.
故正确的有1个.
故选B.
点评:此题主要考查了菱形的判定、梯形的判定、反比例函数的性质、等腰三角形的性质、垂直平分线的性质等知识,熟练记忆相关知识正确区分菱形与矩形,平行四边形与梯形定义是解决问题的关键.
(2)根据反比例函数的性质得出,k>0,每个象限内,y随x的增大而减小,分别讨论得出答案;
(3)根据菱形的判定定理得出答案即可;
(4)根据直角三角形中30°所对的边等于斜边的一半,得出答案;
(5)根据梯形的定义得出,一组对边平行另一组对边不平行的四边形是梯形得出答案;
(6)根据反比例函数的定义得出答案;
(7)根据等腰三角形的性质得出答案.
解答:解:(1)根据垂直平分线的性质,P在AB垂直平分线上,但是O不一定在AB的垂直平分线上,
∴PO不一定是AB垂直平分线,故此选项错误;
(2)根据反比例函数的性质得出,
k>0,每一个象限内y随x的增大而减小,当x1<x2<0时,
∵x1<x2,∴y1>y2;
当0<x1<x2时,∵x1<x2,∴y1>y2;
当x1<0,x2>0,(x1,y1)在第三象限,(x2,y2)在第一象限,
∴y2>y1.故此选项错误;
(3)根据菱形的判定定理得出,对角线互相垂直平分的四边形是菱形,故此选项正确;
(4)根据只有直角三角形中30°所对的边等于斜边的一半,而此三角形不一定是直角三角形,
则AC不一定等于4,故此选项错误;
(5)根据梯形的定义得出,一组对边平行另一组对边不平行的四边形是梯形,故此选项错误;
(6)根据反比例函数的定义,
 是反比例函数,应该k≠0,故此选项错误;
是反比例函数,应该k≠0,故此选项错误;(7)若一个等腰三角形的两边长为2和3,那么它的周长为7,也可能是3+3+2=8,故此选项错误.
故正确的有1个.
故选B.
点评:此题主要考查了菱形的判定、梯形的判定、反比例函数的性质、等腰三角形的性质、垂直平分线的性质等知识,熟练记忆相关知识正确区分菱形与矩形,平行四边形与梯形定义是解决问题的关键.

练习册系列答案
相关题目
 下列说法:
下列说法: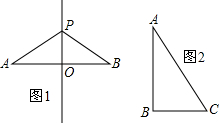
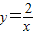 ,(x1,y1),(x2,y2)是其图象上两点,若x1<x2,则y1>y2;
,(x1,y1),(x2,y2)是其图象上两点,若x1<x2,则y1>y2; 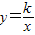 是反比例函数;
是反比例函数;