题目内容
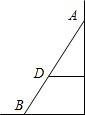AB是斜靠在墙上的长梯，梯角B距墙1.6m，梯上点D距墙1.4m，BD=0.55m，则梯长AB为分析：由DE∥BC可得△ADE∽△ABC，进而利用相似三角形的对应边成比例可得梯子AB的长．
解答：解：∵DE⊥AC，AC⊥CB，
∴DE∥BC，
∴△ADE∽△ABC，
∴
=
，
=
，
解得AB=4.4m．
故答案为4.4．
∴DE∥BC，
∴△ADE∽△ABC，
∴
| AD |
| AB |
| DE |
| BC |
| AB-0.55 |
| AB |
| 1.4 |
| 1.6 |
解得AB=4.4m．
故答案为4.4．
点评：考查相似三角形的应用；用到的知识点为：两角对应成比例且夹角相等的两三角形相似；相似三角形的对应边成比例．
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
如图，AB是斜靠在墙上的长梯，梯脚B距墙1.6m，梯上点D距墙1.4m，BD=0.55m，则梯子的长为多少米？
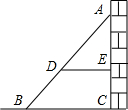如图，AB是斜靠在墙上的长梯，D是梯上一点，梯脚B与墙脚的距离为1.6m（即BC的长），点D与墙的距离为1.4m（即DE的长），BD长为0.55m，则梯子的长为（ ）| A、4.50m | B、4.40m | C、4.00m | D、3.85m |
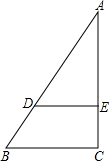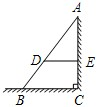如图，AB是斜靠在墙上的长梯，梯脚B距墙脚1.2m，梯上点D距墙0.9m，BD长0.6m，则梯子的长为
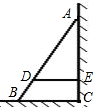如图，AB是斜靠在墙上的长梯，梯脚B距墙脚BC=60cm，梯上点D到AC距离DE=50cm，BD=55cm，求梯子AB的长度．