题目内容
数据21,22,23,24,25,…,40的标准差是σ1,数据302,303,304,305,306,…,321的标准差是σ2,则( )
| A、σ1<σ2 | B、σ1=σ2 | C、σ1>σ2 | D、不能确定σ1、σ2的大小 |
分析:方差是用来衡量一组数据波动大小的量,每个数都加了281波动不会变,方差不变,标准差不变.
解答:解:由题意知,设原来的平均数为
,每个数据都加了281,则平均数变为
+281,
原来的方差s12=
[(x1-
)2+(x2-
)2+…+(xn-
)2]=σ12,
现在的方差s22=
[(x1+281-
-281)2+(x2+281-
-281)2+…+(xn+281-
-281)2]
=
[(x1-
)2+(x2-
)2+…+(xn-
)2]
=σ22,
∴σ12=σ22,
故选B.
. |
| x |
. |
| x |
原来的方差s12=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
现在的方差s22=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
=σ22,
∴σ12=σ22,
故选B.
点评:本题说明了当数据都加上一个数(或减去一个数)时,方差不变,即数据的波动情况不变.当数据都乘以一个数a时,方差变为原来的a2倍.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
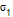 ,数据302,303,304,305,306,…,321的标准差是
,数据302,303,304,305,306,…,321的标准差是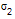 ,则
,则
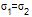

 的大小
的大小