题目内容
(2009•海淀区一模)已知:关于x的一元一次方程kx=x+2 ①的根为正实数,二次函数y=ax2-bx+kc(c≠0)的图象与x轴一个交点的横坐标为1.(1)若方程①的根为正整数,求整数k的值;
(2)求代数式
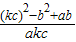 的值;
的值;(3)求证:关于x的一元二次方程ax2-bx+c=0 ②必有两个不相等的实数根.
【答案】分析:(1)根据一元一次方程及根的条件,求k的值.
(2)把交点坐标代入二次函数的解析式求出值.
(3)根据根的判别式和一元一次方程的根为正实数得出x有两不相等的实数根.
解答:解:(1)由kx=x+2,
得(k-1)x=2.
依题意k-1≠0.
∴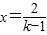 .
.
∵方程的根为正整数,k为整数,
∴k-1=1或k-1=2.
∴k1=2,k2=3.
(2)依题意,二次函数y=ax2-bx+kc的图象经过点(1,0),
∴0=a-b+kc,
kc=b-a,
∵已知akc≠0,
∴b-a≠0,
∴ =
= ,
,
(3)证明:方程②的判别式为△=(-b)2-4ac=b2-4ac.
由a≠0,c≠0,得ac≠0.
(i)若ac<0,则-4ac>0.故△=b2-4ac>0.
此时方程②有两个不相等的实数根.
(ii)证法一:若ac>0,由(2)知a-b+kc=0,
故b=a+kc.
△=b2-4ac=(a+kc)2-4ac
=a2+2kac+(kc)2-4ac
=a2-2kac+(kc)2+4kac-4ac
=(a-kc)2+4ac(k-1)
∵方程kx=x+2的根为正实数,
∴方程(k-1)x=2的根为正实数.
由x>0,2>0,得k-1>0.
∴4ac(k-1)>0.
∵(a-kc)2≥0,
∴△=(a-kc)2+4ac(k-1)>0.
此时方程②有两个不相等的实数根.
证法二:若ac>0,
∵抛物线y=ax2-bx+kc与x轴有交点,
∴△1=(-b)2-4akc=b2-4akc≥0.
(b2-4ac)-(b2-4akc)=4ac(k-1).
由证法一知k-1>0,
∴b2-4ac>b2-4akc≥0.
∴△=b2-4ac>0.此时方程②有两个不相等的实数根.
综上,方程②有两个不相等的实数根.
点评:考查根的判别式与根的关系和二次函数图象性质.
(2)把交点坐标代入二次函数的解析式求出值.
(3)根据根的判别式和一元一次方程的根为正实数得出x有两不相等的实数根.
解答:解:(1)由kx=x+2,
得(k-1)x=2.
依题意k-1≠0.
∴
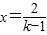 .
.∵方程的根为正整数,k为整数,
∴k-1=1或k-1=2.
∴k1=2,k2=3.
(2)依题意,二次函数y=ax2-bx+kc的图象经过点(1,0),
∴0=a-b+kc,
kc=b-a,
∵已知akc≠0,
∴b-a≠0,
∴
 =
= ,
,(3)证明:方程②的判别式为△=(-b)2-4ac=b2-4ac.
由a≠0,c≠0,得ac≠0.
(i)若ac<0,则-4ac>0.故△=b2-4ac>0.
此时方程②有两个不相等的实数根.
(ii)证法一:若ac>0,由(2)知a-b+kc=0,
故b=a+kc.
△=b2-4ac=(a+kc)2-4ac
=a2+2kac+(kc)2-4ac
=a2-2kac+(kc)2+4kac-4ac
=(a-kc)2+4ac(k-1)
∵方程kx=x+2的根为正实数,
∴方程(k-1)x=2的根为正实数.
由x>0,2>0,得k-1>0.
∴4ac(k-1)>0.
∵(a-kc)2≥0,
∴△=(a-kc)2+4ac(k-1)>0.
此时方程②有两个不相等的实数根.
证法二:若ac>0,
∵抛物线y=ax2-bx+kc与x轴有交点,
∴△1=(-b)2-4akc=b2-4akc≥0.
(b2-4ac)-(b2-4akc)=4ac(k-1).
由证法一知k-1>0,
∴b2-4ac>b2-4akc≥0.
∴△=b2-4ac>0.此时方程②有两个不相等的实数根.
综上,方程②有两个不相等的实数根.
点评:考查根的判别式与根的关系和二次函数图象性质.

练习册系列答案
相关题目