题目内容
如图,将图中线段AB绕点A按顺时针方向旋转90°后,得到线段AB′,则点B′的坐标是 ;在整个旋转过程中,线段AB所扫过的面积为 (结果保留π).
【答案】分析:解题的关键是抓住旋转的三要素:旋转中心点A,旋转方向顺时针,旋转角度90°,通过画图得B′;线段AB在旋转过程中扫过的面积是一个扇形,根据扇形公式计算即可.
解答: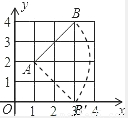 解:由图知A(1,2),B(3,4)根据旋转中心A点,旋转方向顺时针,旋转角度90°,画图,
解:由图知A(1,2),B(3,4)根据旋转中心A点,旋转方向顺时针,旋转角度90°,画图,
从而得B′点坐标为(3,0).
线段AB所扫过的面积为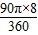 =2π;
=2π;
故答案为:(3,0),2π.
点评:此题考查了坐标与图形变化,用到的知识点是图形的旋转、扇形的面积公式、勾股定理等,关键是抓住旋转的三要素:旋转中心,旋转方向,旋转角度,通过画图确定所求点的坐标.
解答:
 解:由图知A(1,2),B(3,4)根据旋转中心A点,旋转方向顺时针,旋转角度90°,画图,
解:由图知A(1,2),B(3,4)根据旋转中心A点,旋转方向顺时针,旋转角度90°,画图,从而得B′点坐标为(3,0).
线段AB所扫过的面积为
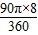 =2π;
=2π;故答案为:(3,0),2π.
点评:此题考查了坐标与图形变化,用到的知识点是图形的旋转、扇形的面积公式、勾股定理等,关键是抓住旋转的三要素:旋转中心,旋转方向,旋转角度,通过画图确定所求点的坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•洛江区质检)如图,将图中线段AB绕点A按顺时针方向旋转90°后,得到线段AB′,则点B′的坐标是
(2012•洛江区质检)如图,将图中线段AB绕点A按顺时针方向旋转90°后,得到线段AB′,则点B′的坐标是
 的值(用含α的式子表示出来)
的值(用含α的式子表示出来) 如图,将图中线段AB绕点A按顺时针方向旋转90°后,得到线段AB′,则点B′的坐标是________;在整个旋转过程中,线段AB所扫过的面积为________(结果保留π).
如图,将图中线段AB绕点A按顺时针方向旋转90°后,得到线段AB′,则点B′的坐标是________;在整个旋转过程中,线段AB所扫过的面积为________(结果保留π).