Question

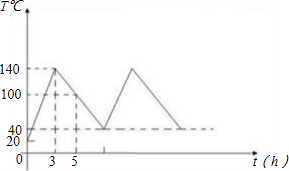
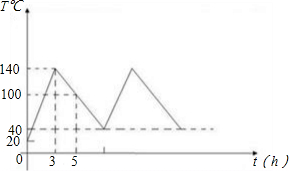
某工厂有一批4800个零件的加工任务，在零件加工过程中，机器温度会持续升高，为了保护机器，当温度达140℃时机器会自动停机降温，当温度达40℃时机器又自动开机加工，如此反复，18个小时后顺利完成任务．当天车间温度为20℃，机器温度变化如图所示．
（1）求第一次降温过程中，机器温度T（℃）与运行时间t（h）的函数关系式；
（2）求第一次停机后多少小时机器开始第二次加工；
（3）经过技术革新，配置一套自动冷却系统，该机器可以不停机连续加工，加工速度提高20%．技术革新后完成这批零件的加工任务需多少小时？

Answer 1

分析：（1）先设函数关系式，再从图中找到时间和温度的对应值，求出自变量，可得机器温度T（℃）与运行时间t（h）的函数关系式；
（2）从函数图象可知机器开始第二次工作时的函数值为40，将其代入函数关系式可求出第一次停机后多少小时机器开始第二次加工；
（3）从函数图象得出原加工时间，再求出原加工速度，据此求出加工速度提高20%后的速度，那么技术革新后加工时间可求．

解答：解：（1）设函数关系式为：y=kx+b由题意得

140=3k+b 100=5k+b

，
解得，k=-20，b=200，
故函数关系式为：y=-20x+200；

（2）当y=40时，机器开始加工，将其代入y=-20x+200中，
解得，x=8（小时），
故第一次停机后8小时机器开始第二次加工；

（3）从函数图象可知机器每次停止工作自动降温的时间为5小时，在18小时中共停止工作自动降温2次，
所以原加工时间为：18-10=8（h），
原加工速度：

4800

8

=600，
技术革新后加工速度：600（1+20%）=720，
加工时间为：

4800

720

=

20

3

h．

点评：本题主要考查一次函数的实际运用，必须学会从一次函数图象中找到对应的已知条件．