题目内容
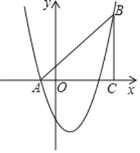
【题目】抛物线y=a（x-1）2+k与x轴两个交点间的距离为2，将抛物线y=a（x-1）2+k向上平移n个单位，平移后的抛物线经过点(m，n)，则m的值是______．
【答案】0或2
【解析】
利用二次函数图象上点的坐标特征可求出抛物线与x轴交点的横坐标，由两个交点间的距离为2可求出k=-a，进而可得出x1，x2的值，再由二次函数图象的变换及二次函数图象上点的坐标特征可求出m的值，此题得解．
解：当y=0时，a（x-1）2+k=0，
解得：x1=1-
，x2=1+，
∴1+-（1-）=2=2，
∴k=-a，
∴x1=0，x2=2．
∵将抛物线y=a（x-1）2+k向上平移n个单位，平移后的抛物线经过点（m，n），
∴m=x1=0或m=x2=2．
故答案为：0或2．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
【题目】某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查，根据每车乘坐人数分为5类，每车乘坐1人、2人、3人、4人、5人分别记为A、B、C、D、E，由调查所得数据绘制了如图所示的不完整的统计图表．
类别 | 频率 |
A | m |
B | 0.35 |
C | 0.20 |
D | n |
E | 0.05 |
(1)求本次调查的小型汽车数量及m，n的值；
(2)补全频数分布直方图；
(3)若某时段通过该路段的小型汽车数量为5000辆，请你估计其中每车只乘坐1人的小型汽车数量．