Question

一个三角形三个角的比为1：2：4，证明：角平分线与对边的交点是一个等腰三角形的顶角．

Answer 1

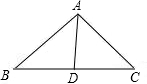证明：如图，∠C：∠B：∠A=1：2：4，AD平分∠BAC且与BC交于点D
设∠C，∠B，∠A分别为x，2x，4x
∵AD平分∠BAC
∴∠BAD=∠DAC=2x
∵∠BAD=∠B=2x
∴△DAB为等腰三角形
∵∠DAC=2x，∠C=x，∠ADC=4x
∴以点D为顶点的等腰三角形只有一个．
分析：设∠C，∠B，∠A分别为x，2x，4x，根据三角形内角和定理及角平分线的性质可求得∠BAD=∠DAC=2x，从而可判定△DAB为等腰三角形．
点评：此题主要考查学生对等腰三角形的判定，三角形内角和定理及角平分线的性质的综合运用能力．