题目内容
【题目】综合与实践--------图形变换中的数学问题
问题情境:
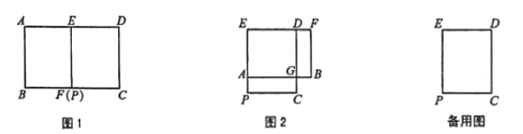
如图1,已知矩形![]() 中,点
中,点![]() 是
是![]() 的中点,连接
的中点,连接![]() .将矩形
.将矩形![]() 沿
沿![]() 剪开,得到四边形
剪开,得到四边形![]() 和四边形
和四边形![]() .
.
(1)求证:四边形![]() 是矩形;
是矩形;
操作探究:
保持矩形![]() 位置不变,将矩形
位置不变,将矩形![]() 从图1的位置开始,绕点
从图1的位置开始,绕点![]() 按逆时针方向旋转,设旋转角为
按逆时针方向旋转,设旋转角为![]() (
(![]() ).操作中,提出了如下向题,请你解答:
).操作中,提出了如下向题,请你解答:
(2)如图2,当矩形![]() 旋转到点
旋转到点![]() 落在线段
落在线段![]() 上时,线段
上时,线段![]() 恰好经过点
恰好经过点![]() ,设
,设![]() 与
与![]() 相交于点
相交于点![]() .判断四边形
.判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)请从![]() 两题中任选一题作答,我选择题.
两题中任选一题作答,我选择题.
A.在矩形![]() 旋转过程中,连接线段
旋转过程中,连接线段![]() 和
和![]() .当
.当![]() 时,直接写出旋转角
时,直接写出旋转角![]() 的度数.
的度数.
B.已知矩形![]() 中,
中,![]() .在矩形
.在矩形![]() 旋转过程中,连接线段
旋转过程中,连接线段![]() 和
和![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)A:60°或300°,B:![]() 或
或![]()
【解析】
(1)由![]() 矩形ABCD的边
矩形ABCD的边![]() 的中点可得ED//FC,ED=FC,根据有一个角是直角的平行四边形是矩形进行解答即可;(2)由(1)可得四边形EPCD为矩形,根据EA=ED即可证明四边形EPCD为正方形;(3)A题①当旋转到如图位置时,连接PF,由AP=BP可得∠PAB=∠PBA,即可证明∠PAE=∠PBF,进而利用SAS可证明△PAE≌△PBF,可得PE=PF,由PE=EF即可证明三角形PEF是等边三角形,可得旋转角∠PEF=60°,②当旋转到如图位置时,连接PF,同①可得∠PEF=60°,可得旋转角为300°;B题:在A题的基础上,①过P作PH⊥EA延长线于H,可得∠HEP=30°,根据∠HEP的三角函数可得HP、HE的长,进而可得AH的长,进而利用勾股定理求出AP的长即可,②过A作AH垂直PE延长线于H,可得∠AEH=30°,根据∠AEH的三角函数可求出AH、HE的长,进而可得PH的长,利用勾股定理求出AP的长即可.
的中点可得ED//FC,ED=FC,根据有一个角是直角的平行四边形是矩形进行解答即可;(2)由(1)可得四边形EPCD为矩形,根据EA=ED即可证明四边形EPCD为正方形;(3)A题①当旋转到如图位置时,连接PF,由AP=BP可得∠PAB=∠PBA,即可证明∠PAE=∠PBF,进而利用SAS可证明△PAE≌△PBF,可得PE=PF,由PE=EF即可证明三角形PEF是等边三角形,可得旋转角∠PEF=60°,②当旋转到如图位置时,连接PF,同①可得∠PEF=60°,可得旋转角为300°;B题:在A题的基础上,①过P作PH⊥EA延长线于H,可得∠HEP=30°,根据∠HEP的三角函数可得HP、HE的长,进而可得AH的长,进而利用勾股定理求出AP的长即可,②过A作AH垂直PE延长线于H,可得∠AEH=30°,根据∠AEH的三角函数可求出AH、HE的长,进而可得PH的长,利用勾股定理求出AP的长即可.
(1)∵四边形ABCD为矩形,
∴AD//BC,AD=BC,∠D=90°,
又∵点E、F是AD、BC的中点,
∴ED//FC,ED=FC,
∴四边形EPCD为平行四边形,
又∵∠D=90°,
∴平行四边形EPCD为矩形.
(2)四边形EAGD是正方形,理由如下:
由(1)得四边形EPCD为矩形,同理可得四边形ABFE为矩形
∴∠E=∠EAB=∠EDG=90°
∴四边形EAGD是矩形
又∵EA=ED
∴矩形EAGD是正方形.
(3)A题:①当旋转到如图位置时,∠PEF为旋转角,连接PF,
∵AP=BP,
∴∠PAB=∠PBA,
∵∠EAB=∠ABF=90°,
∴∠PAE=∠PBF,
∵AE=BF,∠PAE=∠PBF,AP=BP,
∴△PAE≌△PBF,
∴PE=PF,
∵PE=EF,
∴PE=PF=EF,
∴三角形PEF是等边三角形,
∴∠PEF=60°,即旋转角为60°,
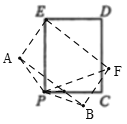
②当旋转到如图位置时,连接PF,
∵AP=BP,
∴∠PAB=∠PBA,
∴∠PAE=∠PBF,
∵AE=BF,∠PAE=∠PBF,PA=PB,
∴△PAE≌△PBF,
∴PF=PE,
∵PE=EF,
∴PE=PF=EF,
∴△PEF是等边三角形,
∴∠PEF=60°,
∴旋转角为360°-60°=300°.

综上所述:旋转角为60°或300°.
B题:①如图,过P作PH⊥EA延长线于H,
由A①得∠PEF=60°,
∵∠AEF=90°,
∴∠HEP=30°,
∴HP=![]() PE=
PE=![]() ×10=5,HE=PE
×10=5,HE=PE![]() cos30°=5
cos30°=5![]() ,
,
∴AH=HE-AE=5![]() -4
-4![]() =
=![]() ,
,
∴AP=![]() =
=![]() =2
=2![]() ,
,

②如图,过A作AH垂直PE延长线于H,
由A②得∠PEF=60°,
∵∠AEF=90°,
∴∠AEH=30°,
∴AH=![]() AE=2
AE=2![]() ,HE=AE
,HE=AE![]() cos30°=6,
cos30°=6,
∴PH=PE+HE=10+6=16,
∴AP=![]() =
=![]() =2
=2![]() .
.

综上所述:AP的长为2![]() 或2
或2![]() .
.