Question

【题目】如图，已知抛物线y=﹣x2+bx+c经过A（0，1）、B（4，3）两点．

（1）求抛物线的解析式；

（2）求tan∠ABO的值；

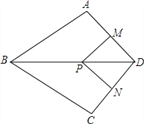
（3）过点B作BC⊥x轴，垂足为C，点M是抛物线上的一个动点，直线MN平行于y轴交直线AB于N，如果M、N、B、C为顶点的四边形是平行四边形，请直接写出M点的横坐标；

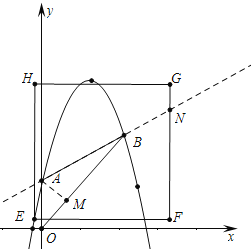
（4）已知点E为抛物线上位于第二象限内任一点，且E点横坐标为m，作边长为10的正方形EFGH，使EF∥x轴，点G在点E的右上方，那么，对于大于或等于﹣1的任意实数m，FG边与过A、B两点的直线都有交点，请说明理由．

Answer 1

【答案】（1）y=﹣x2++1；（2）（3）m=1或3或2+或2﹣．（4）对于大于或等于﹣1的任意实数m，FG边与过A、B两点的直线都有交点，理由见解析

【解析】

试题分析：（1）把A、B两点坐标代入解析式即可解决．

（2）如图作AM⊥OB垂足为M，利用tan∠ABO=解决．

（3）根据MN=BC，列出方程即可解决．

（4）如图只要判断Gy＞Ny即可．

解：（1）由题意，解得，所以抛物线解析式为y=﹣x2++1．

（2）如图作AM⊥OB垂足为M，∵直线AB的解析式为y=x+1，直线OB的解析式为y=x，

∴直线AM为y=﹣2x+1，

由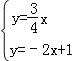解得，

∴直线点M坐标（，）

∴AM= BM=

∴tan∠ABO==．

（3）设点M坐标为（m，﹣m2+m+1），当MN∥BC，MN=BC时，M、N、B、C为顶点的四边形是平行四边形，

∴|﹣m2+m+1﹣（m+1）|=3，

整理得m2﹣4m+3=0或m2﹣4m﹣3=0，

解得m=1或3或2+或2﹣．

（4）如图设FG与直线AB交于点N，

∵点E的横坐标为m，且点E在第二象限，﹣1＜m＜0，

又∵正方形EFGH的边长为10，

∴点F的横坐标为a，9＜a＜10，

∵直线AB的解析式为y=x+1，

∴点N的纵坐标＜Ny＜6，

∵点G的纵坐标11＜Gy＜10，

∴Gy＞Ny，

∴对于大于或等于﹣1的任意实数m，FG边与过A、B两点的直线都有交点．