题目内容
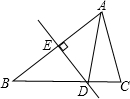
 如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是
如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是
- A.ED=CD
- B.∠DAC=∠B
- C.∠C>2∠B
- D.∠B+∠ADE=90°
D
分析:根据线段垂直平分线的性质得等腰三角形ADB,运用等腰三角形的性质得出尽量多的结论,与各选项进行比对,答案可得.
解答:∵DE是线段AB的垂直平分线,
∴AD=BD.
∴∠B=∠BAD,∠ADE=∠BDE.
∴∠B+∠ADE=90°
其它选项无法证明其是正确的.
故选D
点评:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.利用角的等量代换是正确解答本题的关键.
分析:根据线段垂直平分线的性质得等腰三角形ADB,运用等腰三角形的性质得出尽量多的结论,与各选项进行比对,答案可得.
解答:∵DE是线段AB的垂直平分线,
∴AD=BD.
∴∠B=∠BAD,∠ADE=∠BDE.
∴∠B+∠ADE=90°
其它选项无法证明其是正确的.
故选D
点评:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.利用角的等量代换是正确解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
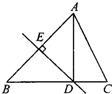 2、如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )
2、如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )