题目内容
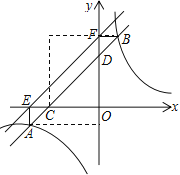
【题目】如图,已知直线y=mx+n与反比例函数![]() 交于A、B两点,点A在点B的左边,与x轴、y轴分别交于点C、点D,AE⊥x轴于E,BF⊥y轴于F
交于A、B两点,点A在点B的左边,与x轴、y轴分别交于点C、点D,AE⊥x轴于E,BF⊥y轴于F
(1)直接写出m、n、k的正负性
(2) 若m=1,n=3,k=4,求直线EF的解析式
(3)写出AC、BD的数量关系,并证明

【答案】(1) m>0、n>0、k>0(2)y=x+4(3)AC=BD
【解析】试题分析:(1)根据函数图象所经过的象限即可判断m、n、k的正负性;(2)先求得点A、B的坐标,再求得点E、F的坐标,用待定系数法求得直线EF的解析式即可;(3)把这两个函数解析式联立,可得mx2+nx-k=0,根据根与系数的关系可得xA+xB=![]() ,令y=0,可得
,令y=0,可得![]() ,所以xA+xB=xC,即可证得结论.
,所以xA+xB=xC,即可证得结论.
试题解析:
(1) m>0、n>0、k>0
(2)联立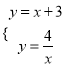 ,解得x1=1,x2=-4
,解得x1=1,x2=-4
∴A(-4,-1)、B(1,4)
∴E(-4,0)、F(0,4)
∴直线EF的解析式为y=x+4
(3)联立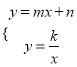 ,整理得mx2+nx-k=0
,整理得mx2+nx-k=0
∴xA+xB=![]()
令y=0,则![]()
∴xA+xB=xC
∴xB+(-xC)=-xA
∴AD=BC(作垂线来理解)
∴AC=BD

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
