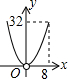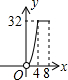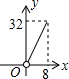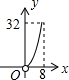题目内容
有四个三角形,分别满足下列条件:
①两角之和等于第三角;
②两边之和等于第三边;
③两角的平方和等于第三个角的平方;
④两边的平方和等于第三边的平方.
其中直角三角形有_______个.
- A.1
- B.2
- C.3
- D.4
B
分析:根据三角形内角和,以及勾股定理的逆定理进行判定即可.
解答:①、两角之和等于第三角;即∠A+∠B=∠C;则2∠C=180°,∠C=90°;
②、两边之和等于第三边,构不成三角形,错误;
③、无此定理;
④、两边的平方和等于第三边的平方,即a2+b2=c2.符合勾股定理的逆定理.
故①④正确,
故选B.
点评:解答此题要用到勾股定理的逆定理:已知三角形ABC的三边满足a2+b2=c2,则三角形ABC是直角三角形.
分析:根据三角形内角和,以及勾股定理的逆定理进行判定即可.
解答:①、两角之和等于第三角;即∠A+∠B=∠C;则2∠C=180°,∠C=90°;
②、两边之和等于第三边,构不成三角形,错误;
③、无此定理;
④、两边的平方和等于第三边的平方,即a2+b2=c2.符合勾股定理的逆定理.
故①④正确,
故选B.
点评:解答此题要用到勾股定理的逆定理:已知三角形ABC的三边满足a2+b2=c2,则三角形ABC是直角三角形.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
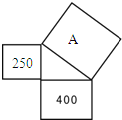 如图,以直角三角形三边为边长作正方形,其中两个以直角边为边长的正方形面积分别为250和400,则正方形A的面积是
如图,以直角三角形三边为边长作正方形,其中两个以直角边为边长的正方形面积分别为250和400,则正方形A的面积是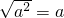
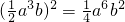
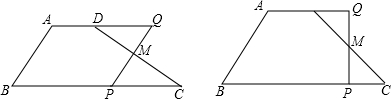
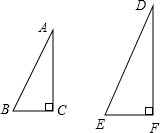 如图,Rt△ABC∽Rt△DEF,∠A=35°,则∠E的度数为
如图,Rt△ABC∽Rt△DEF,∠A=35°,则∠E的度数为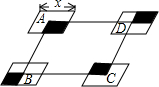 如图,?ABCD的边长为8,面积为32,四个全等的小平行四边形对称中心分别在?ABCD的顶点上,它们的各边与?ABCD的各边分别平行,且与?ABCD相似.若小平行四边形的一边长为x,且0<x≤8,阴影部分的面积的和为y,则y与x之间的函数关系的大致图象是
如图,?ABCD的边长为8,面积为32,四个全等的小平行四边形对称中心分别在?ABCD的顶点上,它们的各边与?ABCD的各边分别平行,且与?ABCD相似.若小平行四边形的一边长为x,且0<x≤8,阴影部分的面积的和为y,则y与x之间的函数关系的大致图象是