题目内容
小东玩一种“挪珠子”游戏,根据挪动珠子的难度不同而得分不同,规定每次挪动珠子的颗数与所得分数的对应关系如下表所示:
| 挪动珠子数(颗) | 2 | 3 | 4 | 5 | 6 | … |
| 所得分数(分) | 5 | 11 | 19 | 29 | 41 | … |
8 n2+n-1
分析:观察不难发现,相邻的两个数的差是连续的偶数,依次计算即可写出所得分数为71分时,所挪动的珠子数;
设挪动n颗珠子时的得分为an,写出相邻的两次得分的表达式,然后根据规律把左右两边分别相加,整理即可得解.
解答:∵11-5=6,
19-11=8,
29-19=10,
41-29=12,
∴挪动7颗珠子所得分数为41+14=55,
挪动8颗珠子所得分数为55+16=71,
故,所得分数为71分时,则挪动的珠子数为8颗;
设挪动n颗珠子时的得分为an,则a2=5,
a3-a2=11-5=6=2×3,
a4-a3=19-11=8=2×4,
a5-a4=29-19=10=2×5,
a6-a5=41-29=12=2×6,
…,
an-an-1=2n,
a2+a3-a2+a4-a3+a5-a4+a6-a5+…+an-an-1=5+2×3+2×4+2×5+2×6+…+2n,
=2×1+2×2+2×3+2×4+2×5+2×6+…+2n-1,
=2(1+2+3+4+5+6+…+n)-1,
=2×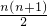 -1,
-1,
=n2+n-1.
故答案为:8,n2+n-1.
点评:本题考查了数字变化规律,观察出相邻两个数的差是连续偶数是解题的关键,求和时把5拆分成(2×1+2×2-1)比较关键.
分析:观察不难发现,相邻的两个数的差是连续的偶数,依次计算即可写出所得分数为71分时,所挪动的珠子数;
设挪动n颗珠子时的得分为an,写出相邻的两次得分的表达式,然后根据规律把左右两边分别相加,整理即可得解.
解答:∵11-5=6,
19-11=8,
29-19=10,
41-29=12,
∴挪动7颗珠子所得分数为41+14=55,
挪动8颗珠子所得分数为55+16=71,
故,所得分数为71分时,则挪动的珠子数为8颗;
设挪动n颗珠子时的得分为an,则a2=5,
a3-a2=11-5=6=2×3,
a4-a3=19-11=8=2×4,
a5-a4=29-19=10=2×5,
a6-a5=41-29=12=2×6,
…,
an-an-1=2n,
a2+a3-a2+a4-a3+a5-a4+a6-a5+…+an-an-1=5+2×3+2×4+2×5+2×6+…+2n,
=2×1+2×2+2×3+2×4+2×5+2×6+…+2n-1,
=2(1+2+3+4+5+6+…+n)-1,
=2×
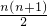 -1,
-1,=n2+n-1.
故答案为:8,n2+n-1.
点评:本题考查了数字变化规律,观察出相邻两个数的差是连续偶数是解题的关键,求和时把5拆分成(2×1+2×2-1)比较关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
小东玩一种“挪珠子”游戏,根据挪动珠子的难度不同而得分不同,规定每次挪动珠子的颗数与所得分数的对应关系如下表所示:
按表中规律,当所得分数为71分时,则挪动的珠子数为 颗; 当挪动n颗珠子时(n为大于1的整数),所得分数为 (用含n的代数式表示).
| 挪动珠子数(颗) | 2 | 3 | 4 | 5 | 6 | … |
| 所得分数(分) | 5 | 11 | 19 | 29 | 41 | … |