题目内容
如图, AB是⊙O的弦,AD="BD," ⊙O的半径是4,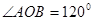 ,则OD=______.
,则OD=______.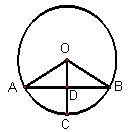
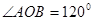 ,则OD=______.
,则OD=______.
2
分析:根据等腰三角形的性质,可以证得OD⊥AB,在直角△AOD中利用三角函数即可求解.
解:∵OA=OB,AD=BD
∴OD⊥AB,∠AOD=
 ∠AOB=60°
∠AOB=60°∴在直角△AOD中,OD=OA?cos∠AOD=4×
 =2.
=2.故答案是:2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
题目内容
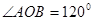 ,则OD=______.
,则OD=______.
 ∠AOB=60°
∠AOB=60° =2.
=2.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案