题目内容
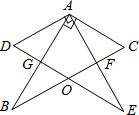
如图所示,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.有以下四个结论:①AF丄BC;②△ADG≌△ACF;③O为BC的中点;④AG:DE=![]() :4,其中正确结论的序是 .(错填得0分,少填酌情给分).
:4,其中正确结论的序是 .(错填得0分,少填酌情给分).

①②③④
解析:∵两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.
∴∠CAF=30°,
∴∠GAF=60°,
∴∠AFB=90°,
①AF丄BC正确;
∵AD=AC,∠DAG=∠CAF,
∠D=∠C=60°,

∴②△ADG≌△ACF正确;
∵△ADG≌△ACF,
∴AG=AF,
∵AO=AO,
∠AGO=∠AFO=90°,
∴△AGO≌△AFO,
∴∠OAF=30°,
∴∠OAC=60°,
∴AO=CO=AC,
BO=CO=AO,
∴③O为BC的中点正确;
假设DG=x,
∵∠DAG=30°,
∴AG=3x,
∴GE=3x,
④AG:DE=3:4正确;
故答案为:①②③④.

练习册系列答案
相关题目
 如图所示,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.有以下四个结论:①AF丄BC;②△ADG≌△ACF;③O为BC的中点;④AG:DE=
如图所示,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.有以下四个结论:①AF丄BC;②△ADG≌△ACF;③O为BC的中点;④AG:DE= 如图所示,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.有以下四个结论:①AF⊥BC;②△ADG≌△ACF;③O为BC的中点;④AG:DE=
如图所示,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.有以下四个结论:①AF⊥BC;②△ADG≌△ACF;③O为BC的中点;④AG:DE=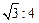 ,其中正确结论的序号是 .
,其中正确结论的序号是 .
 ,其中正确结论的序号是 .
,其中正确结论的序号是 .