Question

解答题：
（1）设互为补角的两个角的差为60°，求较小角的余角．
（2）设一个角的补角是这个角的余角的5倍，求这个角的度数．
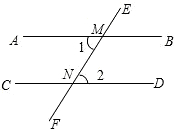
（3）如图，∠1=∠2，∠EMB=55°，试求∠DNF的度数．

（4）如图，△ABC三个顶点分别表示三个小区，AB，BC，AC是连接三个小区的已有自来水管道，某工程队现在要△ABC在内部（包括边上）建一个自来水公司M，M到AB，BC，AC的距离和计为L，已知AB=4，BC=5，AC=6，问自来水供应M在哪个位置，工程对才有最大的经济效益（即L最小）

Answer 1

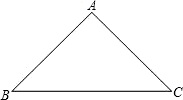
分析：（1）（2）分别利用余角和补角的定义来求，（3）利用平行线的判定和性质来做，（4）设△ABC的内切圆的圆心为M，利用余弦定理和三角形的面积公式，可求出R的长．

解答：（1）30°
解：设较小的角为x，则较大的角为x+60°，
所以x+x+60°=180°，
解得x=60°，
所以较小的角的余角为90°-60°=30°．

（2）67.5°
解：设这个角为x，
所以180°-x=5（90°-x），
解得x=67.5°．

（3）125°
解：∵∠1=∠2，
∴AB∥CD，
又∵∠EMB=55°，
∴∠1=∠2=∠EMB=55°
∴∠DNF=180°-∠2=125°．

（4）由题意可知，点M为△ABC内切圆的圆心时，L最小，
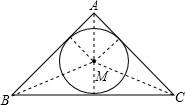在△ABC中，cosB=

AB2+BC2-AC2

2×AB×BC

=

1

8

，
∴sinB=

1- 1 82

=

3 7

8

，
∴△ABC的面积为

1

2

×AB×BC×sinB=

15 7

4

，
设△ABC内切圆的半径为R，则△ABC的面积为

1

2

×(AB+BC+AC)×R=

15 7

4

，
解得R=

7

2

．

点评：（1）-（3）题涉及余角、补角的知识，难度不大，第（4）题，涉及三角形内切圆，余弦定理，三角形面积等知识，并且与实际问题相结合，计算量也比较大，难度偏难．