题目内容
已知,a,b互为相反数,c,d互为倒数,|m|=2,求: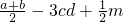 的值.
的值.
解:∵a、b互为相反数,
∴a+b=0
∵c、d互为倒数,
∴cd=1
∵|m|=2,
∴m=±2
当a+b=0,cd=1,m=2时,原式=0-3+ ×2=-2;
×2=-2;
当a+b=0,cd=1,m=-2时,原式=0-3+ ×(-2)=-4.
×(-2)=-4.
分析:求出a+b=0、cd=1、m=±2,分为两种情况:①当a+b=0,cd=1,m=2时,②当a+b=0,cd=1,m=-2时,代入求出即可.
点评:本题考查了代数式的求值、相反数、绝对值、倒数等知识点,关键是得出a+b=0、cd=1、m=±2,题目比较典型,难度适中.
∴a+b=0
∵c、d互为倒数,
∴cd=1
∵|m|=2,
∴m=±2
当a+b=0,cd=1,m=2时,原式=0-3+
 ×2=-2;
×2=-2;当a+b=0,cd=1,m=-2时,原式=0-3+
 ×(-2)=-4.
×(-2)=-4.分析:求出a+b=0、cd=1、m=±2,分为两种情况:①当a+b=0,cd=1,m=2时,②当a+b=0,cd=1,m=-2时,代入求出即可.
点评:本题考查了代数式的求值、相反数、绝对值、倒数等知识点,关键是得出a+b=0、cd=1、m=±2,题目比较典型,难度适中.

练习册系列答案
相关题目