Question

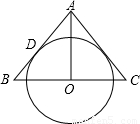
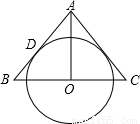
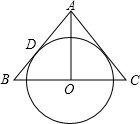如图，AO是△ABC的中线，⊙O与AB边相切于点D．
（1）要使⊙O与AC边也相切，应增加条件（任写一个）；
（2）增加条件后，请你说明⊙O与AC边相切的理由．

Answer 1

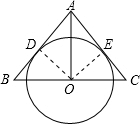（1）解：AB=AC（或∠B=∠C或AO平分∠BAC或AO⊥BC）．

（2）证明：过O作OE⊥AC于E，连OD；
∵AB切⊙O于D，
∴OD⊥AB．
∵AB=AC，AO是BC边上中线，
∴OA平分∠BAC，
又∵OD⊥AB于D，OE⊥AC于E，
∴OE=OD，
∴AC是⊙O的切线．
分析：（1）要使⊙O与AC边也相切，则应满足AO⊥BC，结合已知OB=OC，所以只要符合等腰三角形的三线合一即可；
（2）根据所添加的条件，利用等腰三角形的三线合一即可证明．
点评：熟练掌握切线的判定方法以及等腰三角形的性质．