题目内容
工地上有甲、乙两块铁板，铁板甲形状为等腰三角形，其顶角为a且tana=
，腰长为10cm，铁板乙形状为直角梯形，两底边分别为4cm、10cm，且有一内角为60°，现在我们把它们任意翻转，分别试图从一个直径为8.5cm的圆洞中穿过，结果是（ ）
| 4 |
| 3 |
| A、甲板能穿过，乙板不能穿过 |
| B、甲板不能穿过，乙板能穿过 |
| C、甲、乙两板都能穿过 |
| D、甲、乙两板都不能穿过 |
分析：分别作等腰三角形腰上的高，直角梯形斜腰上的高，求图形的最小宽度，并与直径8.5cm进行比较．
解答：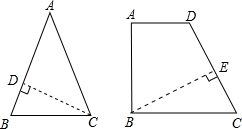
解：设等腰△ABC中，AB=AC=10cm，
作CD⊥AB，垂足为D在Rt△ACD中，tana=
=
，
设CD=4x，则AD=3x，由勾股定理，得
CD2+AD2=AC2，（4x）2+（3x）2=102，
解得x=2，∴CD=4x=8＜8.5，能通过；
在直角梯形ABCD中，AD∥BC，∠B=90°，过B点作BE⊥CD，垂足为E，
∵∠C=60°，BE=BC•sin60°=5
＞8.5，不能通过；故选A．
解：设等腰△ABC中，AB=AC=10cm，作CD⊥AB，垂足为D在Rt△ACD中，tana=
| CD |
| AD |
| 4 |
| 3 |
设CD=4x，则AD=3x，由勾股定理，得
CD2+AD2=AC2，（4x）2+（3x）2=102，
解得x=2，∴CD=4x=8＜8.5，能通过；
在直角梯形ABCD中，AD∥BC，∠B=90°，过B点作BE⊥CD，垂足为E，
∵∠C=60°，BE=BC•sin60°=5
| 3 |
点评：理解并能画出最小宽度，是解答本题的关键．
练习册系列答案
相关题目
，腰长为10cm，铁板乙形状为直角梯形，两底边分别为4cm、10cm，且有一内角为60°，现在我们把它们任意翻转，分别试图从一个直径为8.5cm的圆洞中穿过，结果是
，腰长为10cm，铁板乙形状为直角梯形，两底边分别为4cm、10cm，且有一内角为60°，现在我们把它们任意翻转，分别试图从一个直径为8.5cm的圆洞中穿过，结果是（ ）
，腰长为10cm，铁板乙形状为直角梯形，两底边分别为4cm、10cm，且有一内角为60°，现在我们把它们任意翻转，分别试图从一个直径为8.5cm的圆洞中穿过，结果是（ ）
，腰长为10cm，铁板乙形状为直角梯形，两底边分别为4cm、10cm，且有一内角为60°，现在我们把它们任意翻转，分别试图从一个直径为8.5cm的圆洞中穿过，结果是（ ）