题目内容
已知正△ABC的中心为O,边长为1.将其沿直线l向右不滑动的翻滚一周时,其中心O经过的路径长是( )
分析:作出图形,根据等边三角形的性质求出三角形的顶点到中心的长度,并求出每一次翻滚的角的度数,然后求出△ABC翻滚一周的角度,最后根据弧长的计算公式列式进行计算即可求解.
解答: 解:如图,过点C作CD⊥AB于D,则CD一定经过点O,
解:如图,过点C作CD⊥AB于D,则CD一定经过点O,
∵CD=
BC=
.
∴OC=
CD=
.
根据等边三角形的性质,∠BCD=
∠ACB=
×60°=30°,
∴每一次翻滚中心O旋转的角度为:180°-2×30°=120°,
等边三角形翻滚3次翻滚一周,
∴点O旋转的角度为:120°×3=360°,
∴中心O经过的路径长是:2π•OC=2π×
=
π.
故选B.
 解:如图,过点C作CD⊥AB于D,则CD一定经过点O,
解:如图,过点C作CD⊥AB于D,则CD一定经过点O,∵CD=
| ||
| 2 |
| ||
| 2 |
∴OC=
| 2 |
| 3 |
| ||
| 3 |
根据等边三角形的性质,∠BCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴每一次翻滚中心O旋转的角度为:180°-2×30°=120°,
等边三角形翻滚3次翻滚一周,
∴点O旋转的角度为:120°×3=360°,
∴中心O经过的路径长是:2π•OC=2π×
| ||
| 3 |
| 2 |
| 3 |
| 3 |
故选B.
点评:本题考查了弧长的计算,等边三角形的性质以及旋转变换,作出图形确定出翻滚三次为翻滚一周是解题的关键,本题数形结合的思想更形象直观,且有助于问题的解决.

练习册系列答案
相关题目
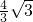 π
π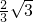 π
π π
π π
π π
π π
π