题目内容
等腰三角形腰长为3,底边长为2,则底角的余弦值为
- A.

- B.
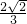
- C.

- D.

A
分析:在△ABC中,AC=BC=3,AB=2,过C作CD⊥AB于D,根据等腰三角形的性质得到BD=1,然后在Rt△DBC中利用余弦的定义即可求出∠B的余弦值.
解答: 解:如图,在△ABC中,AC=BC=3,AB=2.
解:如图,在△ABC中,AC=BC=3,AB=2.
过C作CD⊥AB于D,
则BD=1.
∴cosB= =
= .
.
故选A.
点评:此题主要利用了等腰三角形的性质和余弦函数的定义解决问题.
分析:在△ABC中,AC=BC=3,AB=2,过C作CD⊥AB于D,根据等腰三角形的性质得到BD=1,然后在Rt△DBC中利用余弦的定义即可求出∠B的余弦值.
解答:
 解:如图,在△ABC中,AC=BC=3,AB=2.
解:如图,在△ABC中,AC=BC=3,AB=2.过C作CD⊥AB于D,
则BD=1.
∴cosB=
 =
= .
.故选A.
点评:此题主要利用了等腰三角形的性质和余弦函数的定义解决问题.

练习册系列答案
相关题目