题目内容
【题目】如图，已知矩形ABCD，AB=6，BC=8，E，F分别是AB，BC的中点，AF与DE相交于I，与BD相交于H，则四边形BEIH的面积为（ ）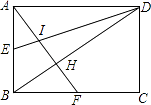
A.
B.
C.
D.
【答案】C
【解析】解：延长AF交DC于Q点，如图所示：
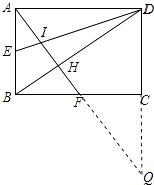
∵E，F分别是AB，BC的中点，
∴AE= 
AB=3，BF=CF= BC=4，
∵四边形ABCD是矩形，
∴CD=AB=6，AB∥CD，AD∥BC，
∴ 
=1，△AEI∽△QDE，
∴CQ=AB=CD=6，△AEI的面积：△QDI的面积=3：12=1：4，
∵AD=8，
∴△AEI中AE边上的高= 
，
∴△AEI的面积= ×3× = 
，
∵△ABF的面积= ×4×6=12，
∵AD∥BC，
∴△BFH∽△DAH，
∴ 
= 
= ，
∴△BFH的面积= ×2×4=4，
∴四边形BEIH的面积=△ABF的面积﹣△AEI的面积﹣△BFH的面积=12﹣ ﹣4= 
．
所以答案是：C．
【考点精析】解答此题的关键在于理解矩形的性质的相关知识，掌握矩形的四个角都是直角，矩形的对角线相等，以及对相似三角形的判定与性质的理解，了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
一诺书业暑假作业快乐假期云南美术出版社系列答案【题目】温州享有“中国笔都”之称，其产品畅销全球，某制笔企业欲将n件产品运往A，B，C三地销售，要求运往C地的件数是运往A地件数的2倍，各地的运费如图所示．设安排x件产品运往A地． 
（1）当n=200时，①根据信息填表：
A地 | B地 | C地 | 合计 | |
产品件数（件） | x | 2x | 200 | |
运费（元） | 30x |
②若运往B地的件数不多于运往C地的件数，总运费不超过4000元，则有哪几种运输方案？
（2）若总运费为5800元，求n的最小值．
