题目内容
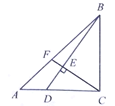
【题目】如图,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() 为边
为边![]() 上一点,且
上一点,且![]() ,连结
,连结![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .若
.若![]() ,则
,则![]() 的长为______.
的长为______.
【答案】![]()
【解析】
作AH⊥BD的延长线于点H,根据已知和勾股定理可求出CD,AD,AB,再根据三角形面积公式,可求出CE的长度,进而可求ED,BE,然后证得△AHD∽△CED,△BEF∽△BHA,根据相似比即可求出答案.
作AH⊥BD的延长线于点H,
∵BC=AC=6,CD=2AD,
∴AD=2,CD=4,
根据勾股定理AB=![]() ,BD=
,BD=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵CE⊥BD,
∴根据勾股定理可得ED=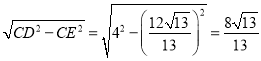 ,
,
∴![]() ,
,
在△AHD与△CED中,∠AHD=∠CED,∠ADH=∠CDE,
∴△AHD∽△CED,
∴![]() ,
,
∴![]() ,
,
根据勾股定理得 ,
,
∴![]() ,
,
在△BEF与△BHA中,∠FBE=∠ABH,∠BEF=∠BHA=90°,
∴△BEF∽△BHA,
∴![]() ,
,
∴![]() ,
,
故答案为![]() .
.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目