题目内容
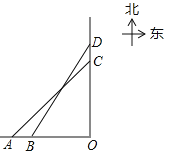
【题目】如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1,60)
【答案】13.5km.
【解析】
试题分析:设B处距离码头Oxkm,分别在Rt△CAO和Rt△DBO中,根据三角函数求得CO和DO,再利用DC=DO﹣CO,得出x的值即可.
试题解析:设B处距离码头Oxkm,在Rt△CAO中,∠CAO=45°,∵tan∠CAO=![]() ,∴CO=AOtan∠CAO=(45×0.1+x)tan45°=4.5+x,在Rt△DBO中,∠DBO=58°,∵tan∠DBO=
,∴CO=AOtan∠CAO=(45×0.1+x)tan45°=4.5+x,在Rt△DBO中,∠DBO=58°,∵tan∠DBO=![]() ,∴DO=BOtan∠DBO=xtan58°,∵DC=DO﹣CO,∴36×0.1=xtan58°﹣(4.5+x),∴x=
,∴DO=BOtan∠DBO=xtan58°,∵DC=DO﹣CO,∴36×0.1=xtan58°﹣(4.5+x),∴x=![]() ≈
≈![]() .因此,B处距离码头O大约13.5km.
.因此,B处距离码头O大约13.5km.

练习册系列答案
相关题目