题目内容
 如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;(2)若OC=3,AB=8,求⊙O直径的长.
解:(1)∵OD⊥AB,垂足为C,交⊙O于点D,
∴弧AD=弧BD,
∵∠AOD=52°,
∴∠DEB= ∠AOD=26°;
∠AOD=26°;
(2)∵OD⊥AB,
∴AC=BC= AB=
AB= ×8=4,
×8=4,
∴在直角三角形AOC中,AO=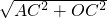 =
=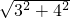 =5.
=5.
∴⊙O直径的长是10.
分析:(1)利用垂径定理可以得到弧AD和弧BD相等,然后利用圆周角定理求得∠DEB的度数即可;
(2)利用垂径定理在直角三角形OAC中求得AO的长即可求得圆的半径.
点评:本题考查了圆周角定理及垂径定理的知识,解题的关键是利用垂径定理构造直角三角形.
∴弧AD=弧BD,
∵∠AOD=52°,
∴∠DEB=
 ∠AOD=26°;
∠AOD=26°;(2)∵OD⊥AB,
∴AC=BC=
 AB=
AB= ×8=4,
×8=4,∴在直角三角形AOC中,AO=
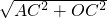 =
=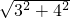 =5.
=5.∴⊙O直径的长是10.
分析:(1)利用垂径定理可以得到弧AD和弧BD相等,然后利用圆周角定理求得∠DEB的度数即可;
(2)利用垂径定理在直角三角形OAC中求得AO的长即可求得圆的半径.
点评:本题考查了圆周角定理及垂径定理的知识,解题的关键是利用垂径定理构造直角三角形.

练习册系列答案
相关题目
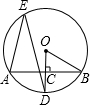 如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=25°,则∠OBA的度数是
如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上,∠AED=25°,则∠OBA的度数是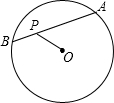 如图,AB是⊙O的一条弦,P是AB上的一点,PA=3,OP=PB=2,则⊙O的半径等于
如图,AB是⊙O的一条弦,P是AB上的一点,PA=3,OP=PB=2,则⊙O的半径等于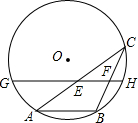 (2013•陕西)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为
(2013•陕西)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为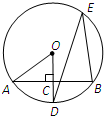 (2008•沈阳)如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(2008•沈阳)如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.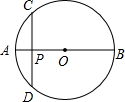 如图,AB是⊙O 的一条直径,CD是⊙O的一条弦,交AB与点P,
如图,AB是⊙O 的一条直径,CD是⊙O的一条弦,交AB与点P,