题目内容
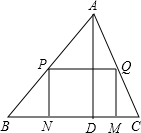如图，△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成矩形零件，使一边在BC上，其余两个顶点分别在边AB、AC上．（1）若这个矩形是正方形，那么边长是多少？
（2）若这个矩形的长是宽的2倍，则边长是多少？
分析：（1）设出边长为xmm，由正方形的性质得出，PQ∥BC，PN∥AD，根据平行线的性质，可以得出比例关系式，
=
、
=
，代入数据求解即可．
（2）设宽为xmm，则长为2xmm，同（1）列出比例关系求解，但是要注意有两种情况，PQ可以为长也可以为宽，分两种情况分别求解即可．
| PN |
| AD |
| BP |
| AB |
| PQ |
| BC |
| AP |
| AB |
（2）设宽为xmm，则长为2xmm，同（1）列出比例关系求解，但是要注意有两种情况，PQ可以为长也可以为宽，分两种情况分别求解即可．
解答：解：（1）设边长为xmm，
∵矩形为正方形，
∴PQ∥BC，PN∥AD，
根据平行线的性质可以得出：
=
、
=
，
由题意知PN=x，AD=80，BC=120，PQ=x，
即
=
，
=
，
∵AP+BP=AB，
∴
+
=
+
=1，
解得x=48．
答：若这个矩形是正方形，那么边长是48mm．
（2）设边宽为xmm，则长为2xmm，
∵PNMQ为矩形，
∴PQ∥BC，PN∥AD，
根据平行线的性质可以得出：
=
、
=
，
①PN为长，PQ为宽：
由题意知PN=2xmm，AD=80mm，BC=120mm，AP=xmm，
即
=
，
=
，
∵AP+BP=AB，
∴
+
=
+
=1，
解得x=30，2x=60．
即长为60mm，宽为30mm．
②PN为宽，PQ为长：
由题意知PN=xmm，AD=80mm，BC=120mm，AP=2xmm，
即
=
，
=
，
∵AP+BP=AB，
∴
+
=
+
=1，
解得x=
，2x=
．
即长为
mm，宽为
mm．
答：矩形的长为60mm，宽是30mm或者长为
mm，宽为
mm．
∵矩形为正方形，
∴PQ∥BC，PN∥AD，
根据平行线的性质可以得出：
| PN |
| AD |
| BP |
| AB |
| PQ |
| BC |
| AP |
| AB |
由题意知PN=x，AD=80，BC=120，PQ=x，
即
| x |
| 80 |
| BP |
| AB |
| x |
| 120 |
| AP |
| AB |
∵AP+BP=AB，
∴
| x |
| 80 |
| x |
| 120 |
| BP |
| AB |
| AP |
| AB |
解得x=48．
答：若这个矩形是正方形，那么边长是48mm．
（2）设边宽为xmm，则长为2xmm，
∵PNMQ为矩形，
∴PQ∥BC，PN∥AD，
根据平行线的性质可以得出：
| PN |
| AD |
| BP |
| AB |
| PQ |
| BC |
| AP |
| AB |
①PN为长，PQ为宽：
由题意知PN=2xmm，AD=80mm，BC=120mm，AP=xmm，
即
| 2x |
| 80 |
| BP |
| AB |
| x |
| 120 |
| AP |
| AB |
∵AP+BP=AB，
∴
| 2x |
| 80 |
| x |
| 120 |
| BP |
| AB |
| AP |
| AB |
解得x=30，2x=60．
即长为60mm，宽为30mm．
②PN为宽，PQ为长：
由题意知PN=xmm，AD=80mm，BC=120mm，AP=2xmm，
即
| x |
| 80 |
| BP |
| AB |
| 2x |
| 120 |
| AP |
| AB |
∵AP+BP=AB，
∴
| x |
| 80 |
| 2x |
| 120 |
| BP |
| AB |
| AP |
| AB |
解得x=
| 240 |
| 7 |
| 480 |
| 7 |
即长为
| 480 |
| 7 |
| 240 |
| 7 |
答：矩形的长为60mm，宽是30mm或者长为
| 480 |
| 7 |
| 240 |
| 7 |
点评：本题考查了正方形以及矩形的性质，结合了平行线的比例关系求解，注意数形结合的运用．
练习册系列答案
相关题目
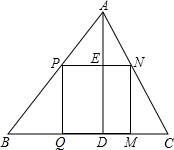如图，△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成正方形零件，使正方形一边在BC上，其余两个顶点分别在AB，AC上，那么这个正方形零件的边长应是
19、如图：△ABC是一块直角三角形余料，∠C=90度，工人师傅把它加工成一个正方形零件，使C为正方形的一个顶点，其余三个顶点分别在AB、BC、AC边上，请你协助工人师傅用尺规画出裁割线．（不写画法，保留作图痕迹）
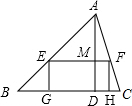如图，△ABC是一块锐角三角形材料，边BC=6cm，高AD=4cm，要把它加工成一个矩形零件，使矩形的一边在BC上，其余两个顶点分别在AB、AC上，要使矩形EGFH的面积最大，EG的长应为
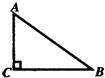19、如图，△ABC是一块直角三角形余料，∠C=90°．工人师傅要把它加工成一个正方形零件，使C为正方形的一个顶点，其余三个顶点分别在AB、BC、AC边上．
如图，△ABC是一块锐角三角形材料，高线AH长8cm，底边BC长10cm，要把它加工成一个矩形零件，使矩形DEFG的一边EF在BC上，其余两个顶点D、G分别在AB、AC上，则四边形DEFG最大面积为（ ）cm2．