Question

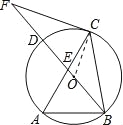
【题目】如图，△ABC内接于⊙O，∠A=60°，点F是直径BD的延长线上一点，且CF=CB．

（1）求∠CBF的度数；

（2）判断直线CF与⊙O的位置关系，并证明；

（3）若AB=3，BC=2，tan∠AEB=3，求线段DE的长．

Answer 1

【答案】（1）∠CBF=30°；

（2）CF是⊙O的切线，证明见解析；

（3）．

【解析】

试题分析：（1）连接OA，根据圆周角定理求出∠BOC，再由OB=OC得出∠OBC=∠OCB=30°，从而求得∠CBF的度数；

（2）由CF=CB得出∠F=30°，进而求得∠BCF=120°，继而由∴∠OCF=∠BCF﹣∠OCB=90°，可得出OC⊥FC，从而得出CF是⊙O的切线．

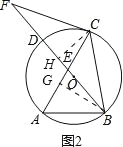
（3）作BG⊥AC于G，CH⊥BF于H，根据直角三角函数和勾股定理求得AE、BE、CE，然后根据相交弦定理就可求得DE的长．

试题解析：（1）连接OC，∵∠A=60°，∴∠BOC=2∠A=120°，又∵OB=OC，

∴∠OBC=∠OCB=30°，即∠CBF=30°．

（2）相切；

理由如下：∵CF=CB，∴∠CBF=∠F=30°，∴∠BCF=120°，

∴∠OCF=∠BCF﹣∠OCB=90°，∴OC⊥FC，∴CF是⊙O的切线．

（3）作BG⊥AC于G，CH⊥BF于H，∵∠A=60°，AB=3，

∴AG=AB=，BG=AB=，∵tan∠AEB=3，∴=3，

∴EG==，∴AE=AG+GE=，∴BE==，

∵∠FBC=30°，BC=2，∴HC=BC=，∵tan∠AEB=3，，∴tan∠HEC=3，

∴=3，，∴HE=，∴EC==，∵DE×BE=CE×AE，

∴DE==．