题目内容
若（m2+n2）（1-m2-n2）+6=0，则m2+n2的值为 ．
考点：换元法解一元二次方程
专题：
分析：设m2+n2=x，把原方程变形，求得x，即可得出m2+n2的数值．
解答：解：设m2+n2=x，则原方程为
x（1-x）+6=0
整理得x2-x-6=0，
（x-3）（x+2）=0
解得x1=3，x2=-2；
∵m2+n2=是非负数，
∴m2+n2=3．
故答案为：3．
x（1-x）+6=0
整理得x2-x-6=0，
（x-3）（x+2）=0
解得x1=3，x2=-2；
∵m2+n2=是非负数，
∴m2+n2=3．
故答案为：3．
点评：此题考查利用换元法解一元二次方程，注意要根据方程的特点灵活选用合适的方法．
练习册系列答案
相关题目
甲、乙两人沿相同的路线由A地到B地匀速前进，A，B两地间的路程为20千米．他们前进的路程为s（单位：千米），甲出发后的时间为t（单位：时），甲、乙前进的路程与时间的函数图象如图所示．根据图象信息，求：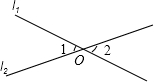
如图，已知直线l1与l2相交于点O，∠1+∠2=100°，那么∠1=
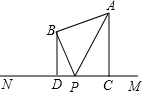如图：两点A、B在直线MN外的同侧，AB=5，A到MN的距离AC=8，B到MN的距离BD=5，P在直线MN上运动，则|PA-PB|的最大值等于
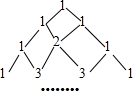仔细观察杨辉三角系数表，按规律写出（a+b）4展开式所缺的系数：