题目内容
13、如图，直线l过正方形ABCD的顶点B，点A、C到直线l的距离分别是a和b，则正方形的面积是a2+b2
．分析：根据AAS可以证明△ABE≌△BCF，得BE=CF=b，根据勾股定理求得直角三角形ABE斜边的平方，即为正方形的面积．
解答：解：∵四边形ABCD是正方形，
∴AB=CB，∠ABC=90°．
又AE⊥l，CF⊥l，
则∠AEB=∠BCF=90°．
∴∠A=∠CBF，
∴△ABE≌△BCF．
∴BE=CF=b．
则正方形的面积=AB2=AE2+BE2=a2+b2．
故答案为，a2+b2．
∴AB=CB，∠ABC=90°．
又AE⊥l，CF⊥l，
则∠AEB=∠BCF=90°．
∴∠A=∠CBF，
∴△ABE≌△BCF．
∴BE=CF=b．
则正方形的面积=AB2=AE2+BE2=a2+b2．
故答案为，a2+b2．
点评：此题综合运用了全等三角形的判定和性质、勾股定理的计算．
练习册系列答案
相关题目
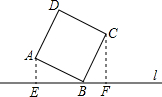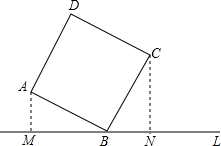如图，直线L过正方形ABCD的顶点B，点A、C到直线L的距离分别是1和2，则正方形的边长是
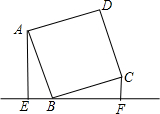如图，直线l过正方形ABCD的顶点B，点A、C到直线l的距离分别是a和b，则正方形的边长是
15、如图，直线l过正方形ABCD的顶点D，过A、C分别作直线l的垂线，垂足分别为E、F．若AE=4a，CF=a，则正方形ABCD的面积为
如图，直线l过正方形ABCD的顶点B，点A，C到直线l的距离分别为1和2，则正方形的边长是（ ）| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
如图，直线d过正方形ABCD的顶点B，点A，C到直线d的距离分别是