题目内容
【题目】如图,将边长为6的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N.
(1)若CM=x,则CH= (用含x的代数式表示);
(2)求折痕GH的长.
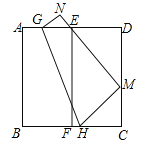
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)利用翻折变换的性质结合勾股定理表示出CH的长即可;
(2)首先得出△EDM∽△MCH,进而求出MC的长,再利用△NEG∽△DEM,求出NG的长,再利用勾股定理得出GH的长.
试题解析:(1)∵CM=x,BC=6,∴设HC=y,则BH=HM=6﹣y,故![]() ,整理得:
,整理得:![]() ,故答案为:
,故答案为:![]() ;
;
(2)∵四边形ABCD为正方形,∴∠B=∠C=∠D=90°,设CM=x,由题意可得:ED=3,DM=6﹣x,∠EMH=∠B=90°,故∠HMC+∠EMD=90°,∵∠HMC+∠MHC=90°,∴∠EMD=∠MHC,∴△EDM∽△MCH,∴![]() ,即
,即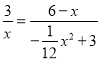 ,解得:
,解得:![]() =2,
=2,![]() =6(不合题意舍去),∴CM=2,∴DM=4,∴在Rt△DEC中,由勾股定理得:EM=5,∴NE=MN﹣EM=6﹣5=1,∵∠NEG=∠DEM,∠N=∠D,∴△NEG∽△DEM,∴
=6(不合题意舍去),∴CM=2,∴DM=4,∴在Rt△DEC中,由勾股定理得:EM=5,∴NE=MN﹣EM=6﹣5=1,∵∠NEG=∠DEM,∠N=∠D,∴△NEG∽△DEM,∴![]() ,∴
,∴![]() ,解得:NG=
,解得:NG=![]() ,由翻折变换的性质,得AG=NG=
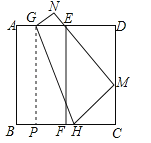
,由翻折变换的性质,得AG=NG=![]() ,过点G作GP⊥BC,垂足为P,则BP=AG=
,过点G作GP⊥BC,垂足为P,则BP=AG=![]() ,GP=AB=6,当x=2时,CH=
,GP=AB=6,当x=2时,CH=![]() ,∴PH=BC﹣HC﹣BP=
,∴PH=BC﹣HC﹣BP=![]() =2,在Rt△GPH中,GH=
=2,在Rt△GPH中,GH=![]() =
=![]() =
=![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如表:
(1)把表中所空各项数据填写完整;
选手 | 选拔成绩/环 | 中位数 | 平均数 | |||||
甲 | 10 | 9 | 8 | 8 | 10 | 9 | ||
乙 | 10 | 10 | 8 | 10 | 7 | 9 | ||
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
【题目】某商场一天中售出李宁牌运动鞋11双,其中各种尺码的鞋的销售量如表所示,则这11双鞋的尺码组成一组数据中位数为_____.
鞋的尺码(单位:厘米) | 23.5 | 24 | 24.5 | 25 | 26 |
销售量(单位:双) | 1 | 2 | 2 | 5 | 1 |
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的9折出售,B型台灯按标价的8折出售,那么这批台灯全部售出后,商场共获利多少元?